Vícevrstvý Perceptron
Vícevrstvý Perceptron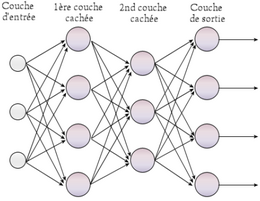 Vícevrstvý perceptron
Vícevrstvý perceptron
| Podtřída | Neuronová síť pro dopředné šíření |
|---|---|
| Vynálezce | Frank Rosenblatt |
Perceptronových ( MLP) je typ umělé neuronové sítě organizovaného v několika vrstvách, v nichž údaje proudí od vstupní vrstvy pouze na výstupní vrstvě; jedná se tedy o dopřednou síť . Každá vrstva je tvořena proměnným počtem neuronů, přičemž neurony poslední vrstvy (nazývané „výstup“) jsou výstupy celého systému.
Perceptron byl vynalezen v roce 1957 o Frank Rosenblatt na Cornell letecké laboratoře . V této první verzi byl perceptron poté jednovrstvý a měl pouze jeden výstup, ke kterému byly připojeny všechny vstupy.
Vícevrstvá zpětná propagace perceptron
První neuronové sítě nebyly schopny vyřešit nelineární problémy; Toto omezení bylo odstraněno přes backpropagation chybové gradientu ve vícevrstvých systémech, navržených Paul Werbos (en) v roce 1974 a vytvořil dvanáct let později, v roce 1986 by David Rumelhart (EN) .
Ve vícevrstvém zpětně se množícím perceptronu jsou neurony v jedné vrstvě spojeny se všemi neurony v sousedních vrstvách. Tyto vazby jsou vystaveny koeficientu, který mění účinek informace na cílový neuron. Hmotnost každého z těchto odkazů je tedy klíčovým prvkem ve fungování sítě: instalace vícevrstvého Perceptronu k vyřešení problému proto zahrnuje stanovení nejlepších vah použitelných pro každé z inter-neuronálních spojení. Zde se toto stanovení provádí pomocí algoritmu zpětného šíření .
Algoritmus šíření
Váhy jsou zastoupeny v maticích a poté přeneseny do další vrstvy, například:
Ž=(w11⋯w1ne⋮⋱⋮wm1⋯wmne) a B=(b1⋮bm){\ displaystyle W = {\ begin {pmatrix} w_ {11} & \ cdots & w_ {1n} \\\ vdots & \ ddots & \ vdots \\ w_ {m1} & \ cdots & w_ {mn} \ end { pmatrix}} {\ text {et}} B = {\ begin {pmatrix} b_ {1} \\\ vdots \\ b_ {m} \ end {pmatrix}}} y=σ(ŽX+B){\ displaystyle y = \ sigma (Wx + B)}Učení se
Výpočet chybyZnalostí očekávané hodnoty na výstupu perceptronu pro dané vstupy můžeme vypočítat odchylku od predikce díky objektivní funkci , nejčastěji střední kvadratické chybě (zkráceně ), jako například:
;Tato funkce není lineární a její derivace je větší, pokud je předpověď daleko od očekávané hodnoty, což umožňuje rychlejší učení. Naopak absolutní střední chyba ( ) má konstantní derivaci, a proto se rychlost učení, která se nemění:
;Minimalizací těchto objektivních funkcí se předpovědi zpřesňují.
Výpočet gradientuBěhem fáze učení, po výpočtu chyb neuronové sítě, je nutné je opravit, aby se zlepšil její výkon. K minimalizaci těchto chyb - a tedy objektivní funkce - se nejčastěji používá algoritmus gradientu . Gradient se počítá s cílem zjistit kolísání cílové funkce s ohledem na parametry . Poté umožňuje upravit tyto parametry v poměru k jejich dopadu na přesnost predikce s cílem dosáhnout po několika iteracích celkového minima objektivní funkce.
Úprava parametrů v daném okamžiku se provádí například:
θt+1=θt-α∇VS,{\ displaystyle \ theta _ {t + 1} = \ theta _ {t} - \ alpha \ nabla C,}se na skalární , rychlosti učení a gradientu cílové funkce. Algoritmus přechodu proto umožňuje najít parametry sítě tak, aby součet chyb způsobených předpovědi na tréninkových datech byl co nejnižší, to znamená, že:
VSX(θ)=minθVSX(θ).{\ displaystyle C_ {X} (\ theta) = \ min _ {\ theta} C_ {X} (\ theta).}Gradient se počítá s parciální derivací objektivní funkce s ohledem na každý z parametrů. Když existuje několik parametrů, které mají být optimalizovány, je to vyjádřeno jako vektor, někdy známý , poté přidaný do vektoru parametrů poté, co byl vynásoben rychlostí učení. Gradient označuje směr k maximu objektivní funkce a jeho protiklad proto vede k minimu. Jeho výraz je tedy:
∇VSX(θ)=(∂VS∂θ1∂VS∂θ2∂VS∂θ3⋯)T{\ displaystyle \ nabla C_ {X} (\ theta) = {\ begin {pmatrix} {\ dfrac {\ parciální C} {\ parciální \ theta _ {1}}} & {\ dfrac {\ parciální C} {\ částečná \ theta _ {2}}} & {\ dfrac {\ částečná C} {\ částečná \ theta _ {3}}} & \ cdots \ end {pmatrix}} ^ {T}}Nechť je gradient na perceptronu vrstvy , pak lze sadu gradientů této vrstvy uložit a manipulovat s ní v Jacobově matici , to znamená matici obsahující parciální derivace funkce vektoru cíle přes celou vrstvu, s :
Jk=(∇1∇2∇3⋮∇m)=(∂VS∂θ1,1⋯∂VS∂θ1,ne⋮⋱⋮∂VS∂θm,1⋯∂VS∂θm,ne){\ displaystyle J_ {k} = {\ begin {pmatrix} \ nabla _ {1} \\\ nabla _ {2} \\\ nabla _ {3} \\\ vdots \\\ nabla _ {m} \ konec {pmatrix}} = {\ start {pmatrix} {\ dfrac {\ částečná C} {\ částečná \ theta _ {1,1}}} & \ cdots & {\ dfrac {\ částečná C} {\ částečná \ theta _ {1, n}}} \\\ vdots & \ ddots & \ vdots \\ {\ dfrac {\ částečné C} {\ částečné \ theta _ {m, 1}}} & \ cdots & {\ dfrac {\ částečné C} {\ částečné \ theta _ {m, n}}} \ konec {pmatrix}}} ;Při použití věty o odvození složené funkce je variace objektivní funkce vzhledem k jedné z vah:
;S částečnou derivací aktivační funkce a částečnou derivací objektivní funkce s ohledem na konečnou předpověď . Rozvíjením a používáním pravidla odvozování součtů :
; , pokud je funkce sigmoidu použita jako aktivace nebo pro hyperbolický tangens; ;Učení se zastaví, když se parametry sbíhají k hodnotám a derivace objektivní funkce se rovná 0.
Algoritmus zpětného šíření
- Prezentace tréninkového vzoru v síti.
- Porovnání síťového výstupu s cíleným výstupem.
- Výpočet chyby na výstupu každého z neuronů sítě.
- Výpočet výstupní hodnoty pro každý z neuronů, která by byla správná.
- Definice zvýšení nebo snížení nezbytného k získání této hodnoty (místní chyba).
- Přizpůsobení hmotnosti každého připojení směrem k nejmenší místní chybě.
- Přiřazení viny všem předchozím neuronům.
- Začněte znovu od kroku 4, u předchozích neuronů použijte vinu jako chybu.
Podívejte se také
Poznámky a odkazy
- Rumelhart, DE, Hinton, McClelland a Williams, RJ (1986), ―Učení interních reprezentací pomocí šíření chyb‖ Parallel Distributed Processing: Explorations in the Microstructure of Cognition
- (in) Shiva Verma , „ Pochopení různých funkcí ztráty pro neuronové sítě. » , Na médiu ,23. dubna 2020(zpřístupněno 13. března 2021 )
- (in) Muhammad Zeeshan Mulla , „ Náklady, aktivace, ztráta funkce || Neuronová síť || Hluboké učení. Co to je? » , Na médiu ,5. května 2020(zpřístupněno 13. března 2021 )
- (en-US) „ Mean Squared Error: Definition and Example “ , od Statistics How To (přístup k 13. března 2021 )
- (in) Prince Grover , „ 5 funkcí regrese ztráty stroje, které by měli všichni studenti vědět “ na médiu ,31. prosince 2020(zpřístupněno 13. března 2021 )
- (in) Shuyu Luo , „ Optimalizace: Funkce ztráty pod kapotou (část I) “ na médiu ,14. října 2018(zpřístupněno 13. března 2021 )
- (in) Niklas Donges, „ Gradient Descent: An Introduction to 1 of Machine Learning Algorithms's most popular “ on Built In ,16. června 2019(zpřístupněno 28. března 2021 )
- (in) Nikil Reddy, „ Jak funguje algoritmus gradientního klesání ve strojovém učení? » , Na Analytics Vidhya ,2. října 2020(zpřístupněno 28. března 2021 )
- (en-US) Imad Dabbura , „ Algoritmus přechodu a jeho varianty “ , na Imad Dabbura ,21. prosince 2017(zpřístupněno 28. března 2021 )
- (in) Směrem k týmu AI , „ Gradient Descent for Machine Learning (ML) 101 with Python Tutorial “ na médiu ,8. ledna 2021(k dispozici na 1. st duben 2021 )
- (in) Anjana Yadav , „ Proč přecházíme na opačné přechody v přechodu? » , Na médiu ,20. února 2020(k dispozici na 1. st duben 2021 )
- (in) Shikhar Goswami , „ Proč je směr nejstrmějšího klesání vždy opačný k gradientu ztrátové funkce? » , Na médiu ,23. června 2020(k dispozici na 1. st duben 2021 )
- (in) Matthew Barnett, „ Primer on Matrix Calculus, Part 2: Jacobians and other fun - LessWrong “ on Less Wrong ,15. srpna 2019(k dispozici na 1. st duben 2021 )
- (in) Julien Herzen , „ Computing the Jacobian matrix of neuron network in Python “ on Medium ,19. listopadu 2018(k dispozici na 1. st duben 2021 )
- (in) Chi Feng Wang , „ Ruční výpočet sestupného přechodu “ na médiu ,25. října 2018(zpřístupněno 14. března 2021 )
Bibliografie
- Marc Parizeau, Neural Networks (The multilayer perceptron and its error retropropagation algorithm) , Université Laval, Laval, 2004, 272 p.
- Fabien Tschirhart (r. Alain Lioret) , Formální neurální sítě aplikované na umělou inteligenci a hry , ESGI (diplomová práce v oblasti multimédií a digitální animace) , Paříž, 2009, 121 s. [ online brief (stránka konzultována 8. listopadu 2010)]


 y=σ(ŽX+B){\ displaystyle y = \ sigma (Wx + B)}
y=σ(ŽX+B){\ displaystyle y = \ sigma (Wx + B)}































