Binomická hromada
Ve výpočtu , je binomické haldy je datová struktura velmi podobná binární haldy , ale také umožňuje dvě hromady, které mají být sloučeny rychle. Podporuje tedy následující operace, vše v O (log n) :
- Vložte do haldy novou položku
- Najděte položku nejmenšího klíče
- Odstraňte položku s nejmenším klíčem z haldy
- Snižte klíč daného prvku
- Odstraňte danou položku z haldy
- Sloučte dvě hromady do jedné
Binomická halda je tedy implementací abstraktního typu sloučitelné haldy , tj . Prioritní fronty umožňující operace sloučení.
Koncept binomického stromu
Binomická halda je ve skutečnosti sada binomických stromů (pro srovnání s binární hromadou, která odpovídá jedinému binárnímu stromu ). Binomické strom je definována rekurzivně takto:
- Binomický strom řádu 0 je jednoduchý uzel
- Binomický strom řádu k má kořen stupně k a jeho děti jsou kořeny binomických stromů řádu k -1, k -2,…, 2, 1, 0 (v tomto pořadí)
Binomický strom řádu k lze také zkonstruovat ze dvou stromů řádu k-1 tak, že jeden z nich je dítětem nejvíce vlevo od kořene druhého. Binomický strom řádu k má 2 k uzly a má výšku k .
Varianty binomických stromů se také používají ke konstrukci haldy Fibonacci .
Binomická halda struktura
Binomická halda je implementována jako sada binomických stromů splňujících vlastnosti binomických hromad :
- Každý binomický strom v haldě má uspořádanou strukturu haldy : klíč každého uzlu je větší nebo roven klíči jeho rodiče.
- Pro každé přirozené celé číslo j existuje nanejvýš jedna binomická hromada řádu j .
První vlastnost označuje, že kořen každého binomického stromu má nejmenší klíč ve stromu. Druhá vlastnost naznačuje, že binomická halda obsahující n prvků se skládá maximálně z ln n + 1 binomických stromů. Ve skutečnosti je počet a pořadí těchto stromů jednoznačně určeno počtem n prvků: každá binomická halda odpovídá bitu 1 v binárním zápisu čísla n . Například 13 odpovídá 1101 v binárním formátu , a proto binomická hromada s 13 prvky bude sestávat ze 3 binomických stromů příslušných řádů 3, 2 a 0 (viz obrázek níže) Kořeny binomických stromů jsou uloženy v seznamu indexovaném podle stromu objednat.
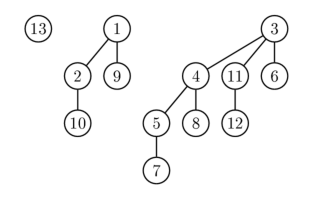
Příklad binomické hromady obsahující klíčové prvky 1, 2, ..., 13. Halda se skládá ze 3 binomických stromů řádu 0, 2 a 3.
Provádění operací
Snad nejzajímavější je operace sloučení dvou hald a je znovu použita ve většině ostatních operací. Kořenové seznamy těchto dvou hromad se prohledávají současně, stejně jako druh sloučení . Pokud pouze jedna ze dvou hromad obsahuje strom řádu j , přidá se do sloučené hromady. Pokud dvě hromady obsahují strom řádu j , spojí se tyto dva stromy do stromu řádu j +1 při respektování struktury haldy (větší ze dvou kořenů se stane dcerou menších). Všimněte si, že možná budeme muset sloučit tento strom se stromem řádu j + 1 přítomným v jedné ze dvou počátečních hromad. Během algoritmu zkoumáme nejvýše 3 stromy každého řádu (dva ze dvou sloučených hromad a jeden vytvořený ze dvou menších stromů). Maximální pořadí stromu je však ln n, a proto je složitost fúze v O (ln n) .
Chcete-li vložit nový prvek do haldy, jednoduše vytvoříme novou haldu obsahující pouze tento prvek, který pak sloučíme s počáteční haldou, a to v O (ln n) .
Chcete-li najít nejmenší prvek haldy, stačí najít minimum mezi kořeny binomických stromů (při maximálním počtu ln n ), což se provádí ještě jednou v O (ln n) .
Chcete - li odebrat nejmenší prvek z haldy, nejprve najdeme tento prvek a odstraníme jej ze svého binomického stromu. Poté získáme seznam jejích podstromů, které transformujeme do jiné binomické haldy a poté sloučíme s předchozí haldou.
Když někdo zmenší klíč položky, může se zmenšit na menší než její otec, čímž poruší hromádku stromu. V tomto případě vyměníme prvek s jeho otcem, dokonce i s jeho dědečkem, a tak dále, dokud se strom znovu neobjedná v hromadě. Každý binomický strom s maximální velikostí ln n je operace v O (ln n) .
Nakonec, abychom odstranili prvek, dáme jej pro klíč mínus nekonečno (menší než všechny ostatní klíče ...), pak odstraníme nejmenší prvek z haldy, to znamená sám.
Reference
- (fr) Tento článek je částečně nebo zcela převzat z článku anglické Wikipedie s názvem „ Binomická halda “ ( viz seznam autorů ) .
- (en) Thomas H. Cormen , Charles E. Leiserson a Ronald L. Rivest , Úvod do algoritmů , MIT Press ,1990[ detail vydání ]
- (en) J. Vuillemin, „ Datová struktura pro manipulaci s prioritními frontami “, in Communications of the ACM 21 (1978), 309-314.
