Skalární součin

V matematiky , a přesněji v algebře a vektorové geometrie je skalární součin je algebraická operace přidá se zákony se vztahují na vektory . Je to bilineární, symetrická, pozitivně určitá forma . Se dvěma vektory spojuje skalární , to znamená číslo jako ty, které definují tento vektorový prostor - reálný pro skutečný vektorový prostor.

Pokud a jsou dva vektory na vektorovém prostoru E na tělo ℝ reálná čísla, pak je skalární součin u které V je skalární (to znamená, že prvek ℝ), označená ∙ , , , nebo . Skalární součin je dán vztahem :, tj. Součin norem vektorů a kosinu úhlu tvořeného dvěma vektory. $\ overrightarrow {u}$ ${\ displaystyle {\ overrightarrow {v}}}$ $\ overrightarrow {u}$ ${\ displaystyle {\ overrightarrow {v}}}$ ${\ displaystyle ({\ overrightarrow {u}} | {\ overrightarrow {v}})}$ ${\ displaystyle \ langle {\ overrightarrow {u}} | {\ overrightarrow {v}} \ rangle}$ ${\ displaystyle \ langle {\ overrightarrow {u}}, {\ overrightarrow {v}} \ rangle}$ ${\ displaystyle {\ overrightarrow {u}} \ cdot {\ overrightarrow {v}} = || {\ overrightarrow {u}} || \ times || {\ overrightarrow {v}} || \ times \ cos ({ \ widehat {{\ overrightarrow {u}}, {\ overrightarrow {v}}}})}$ $\ overrightarrow {u}$ ${\ displaystyle {\ overrightarrow {v}}}$

Tečkový produkt umožňuje využít pojmy tradiční euklidovské geometrie : délky , úhly , ortogonality v dimenzi dva a tři, ale také je rozšířit do reálných vektorových prostorů jakékoli dimenze a (s určitými úpravami v definici) komplexovat vektorové prostory.

Tato operace se nazývá „ produkt “ kvůli určitým vlastnostem (distributivita při přidání, bilinearita), ale není to jediný produkt, který lze spojit se dvěma vektory - viz například křížový produkt , jehož některé vlastnosti souvisejí s tečkou produkt.

Jelikož existují dva hlavní způsoby definování vektorů, buď čistě algebraickým přístupem (viz článek „ Vektorový prostor “), nebo geometrickým přístupem pomocí bipoinů (nebo dvojic bodů, viz „ Vektor “), existují také dva způsoby prezentace skalárního součinu: algebraický způsob (předmět článku „ Prehilbertianův prostor “) a geometrický způsob využívající bipointy.

Historicky se bodový produkt geometricky prezentoval v tradičním euklidovském prostoru, než se pojem rozšířil na jakýkoli skutečný vektorový prostor.

Pojem skalární součin se zobecňuje na komplexní vektorový prostor . V tomto případě skalární produkt již není bilineární formou, ale seskvilineární formou . Mluvíme o hermitovském skalárním produktu .

Přehled aplikací bodových produktů

Produkt dot má několik aplikací. Ve fyzice se například používá k modelování práce síly .

V analytické geometrii umožňuje určit kolmý charakter dvou přímek nebo přímky a roviny . Tato doména je předmětem tohoto článku. V případě jakékoli konečné dimenze má mnoho algebraických aplikací: umožňuje klasifikovat kvadrics , nabízí nástroje pro redukci endomorfismů nebo je základem několika statistických technik , jako je metoda nejmenších čtverců nebo l ' hlavní složka analýza . V geometrii dává vektorovému prostoru metrickou prostorovou strukturu s mnoha vlastnostmi, jako je úplnost .

Tečkový součin se používá také v prostorech nekonečné dimenze, poté umožňuje řešení parciálních diferenciálních rovnic . Teorie se stává jemnější a mnoho výsledků, pravdivých v konečné dimenzi, má jinou podobu.

Na závěr článek „ Euklidovská geometrie “ nabízí syntézu historie, implikací a aplikací skalárního součinu v konečné dimenzi.

Fragmenty historie

Skalární součin, který je důležitým prvkem výpočtu v euklidovské geometrii, se v historii matematiky objevuje poměrně pozdě. Stopy po něm najdeme v Hamiltonu v roce 1843, kdy vytvořil tělo čtveřic, a v Grassmannovi . Peano ji poté definuje v souvislosti s výpočtem plochy nebo determinantu . Roberto Marcolongo a Cesare Burali-Forti to definují pouze pomocí kosinu úhlu a dávají mu název vnitřního produktu nebo tečkového produktu . Právě v této formě se objevuje poté. Jeho symetrická bilineární forma bude poté využita v lineární algebře a jako vlastnost se stane definicí.

Bodování bodového produktu pomocí tečky nebo křížku pochází od Josiaha Willarda Gibbse v 80. letech 19. století.

Výrazový tečkovaný produkt se však poprvé objevuje ve vědecké publikaci v knize Williama Kingdona Clifforda z roku 1878. Toto autorství nicméně zpochybňuje MJ Crowe, pro kterého je Cliffordova práce přechodem mezi kvaternionovou algebrou popsanou Hamiltonem a formalizací vektorových prostorů.

Definice a první vlastnosti

V této části budeme uvažovat o tradičním prostoru definovaném Euklidem: o rovině nebo prostoru tvořeném body, ve kterých jsou známy pojmy vzdálenost a úhel. Víme také, jak vypočítat kosinus libovolného geometrického úhlu. Teorém Pythagoras je Kosinová věta a lze také použít teorém Thales . Geometrická konstrukce vektorů v takovém prostoru je podrobně popsána v článku „ Vektor “.

Dovolit být dva vektory reprezentované bipointy stejného původu $( O , A )$ a $( O , B )$ . Tito zástupci existují bez ohledu na výběr vektorů. Ve zbytku článku je délka bipointu $( O , A )$ označena jako $OA$ nebo někdy $| OA |$ , takže se jedná o kladné reálné číslo.

Vzhledem k bodům $O$ , $A$ a $B$ uvažujeme vektory a . $\ overrightarrow {OA}$ $\ overrightarrow {OB}$

Jsou-li tyto vektory nenulové, je bodovým součinem reálné číslo , kde $θ$ představuje míru geometrického úhlu . $OA \ krát OB \ krát \ cos (\ theta)$ $\ widehat {AOB}$

Pokud je jeden z vektorů nula, pak je bodový produkt nulový.

Ve všech případech označujeme tento skalární součin: $\ overrightarrow {OA} \ cdot \ overrightarrow {OB}$

Bez obav z definování souřadnicového systému a pojmenování bodů můžeme říci, že skalární součin 2 vektorů a je dán vztahem: $\ overrightarrow {u}$ ${\ displaystyle {\ overrightarrow {v}}}$ ${\ displaystyle {\ overrightarrow {u}} \ cdot {\ overrightarrow {v}} = || {\ overrightarrow {u}} || \ times || {\ overrightarrow {v}} || \ times \ cos ({ \ widehat {{\ overrightarrow {u}}, {\ overrightarrow {v}}}})}$

Pokud žádný z vektorů není nula, má tato definice následující podobu:

\ overrightarrow {OA} \ cdot \ overrightarrow {OB} = OA \ krát OB \ krát \ cos (\ widehat {AOB})

Zde, $protože$ ukazuje matematickou funkci kosinus a představuje vrchol geometrického úhlu $O$ , vedenou přes body , $O$ a $B$ . $\ widehat {AOB}$

V případě, že jsou dva vektory stejné, použije se následující notace:

\ overrightarrow {OA} \ cdot \ overrightarrow {OA} = {\ overrightarrow {OA}} ^ {2} = OA ^ {2}

Hodnota tečkového součinu pak odpovídá ploše čtverce s postranní $OA$ .

Euklidovská norma vektoru reprezentované bipoint $AB$ je vzdálenost od $A$ do $B$ ,. Obecně je třeba poznamenat . Je rovna druhé odmocnině tečkového součinu vektoru s sebou: ${\ displaystyle \ left \ | {\ overrightarrow {AB}} \ right \ |}$

\ left \ | \ overrightarrow {AB} \ right \ | = {\ sqrt [{}] {\ overrightarrow {AB} \ cdot \ overrightarrow {AB}}}

Zjevná nerovnost je ověřena takto definovaným skalárním součinem:

Cauchy-Schwarzova nerovnost - Nechť $O$ , $A$ a $B jsou$ tři body roviny, absolutní hodnota skalárního součinu dvou vektorů konců $O$ , $A$ a $O$ , $B$ je vždy menší nebo rovna součinu normy dvou vektorů. Toto zvýšení je napsáno:

{\ displaystyle \ left | {\ overrightarrow {OA}} \ cdot {\ overrightarrow {OB}} \ right | \ leqslant \ left \ | {\ overrightarrow {OA}} \ right \ | \ times \ left \ | {\ overrightarrow {OB}} \ right \ |.}

Rovnost nastane tehdy a jen tehdy, pokud jsou tři body zarovnány.

Toto zvýšení vychází ze skutečnosti, že kosinová funkce bere své hodnoty v intervalu [–1, 1]. Aby se rovnost mohla uskutečnit, je nutné a dostačující, aby kosinus měl hodnotu buď 1 nebo –1, to znamená, že úhel je nula nebo plochý, což znamená, že tři body jsou zarovnány. Tato nerovnost je předmětem článku „ Cauchy-Schwarzova nerovnost “, který rovněž předpokládá jinou algebraickou formalizaci, než je zde zvolená.

Geometrické vlastnosti

Předpokládané

Předchozí definice předpokládá, že je známa definice kosinové funkce . Je možné se této funkci vyhnout.

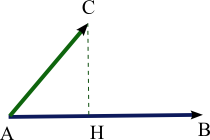
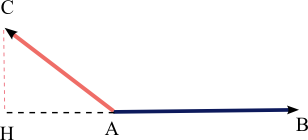
Nechť $A$ , $B$ a $C$ , tři odlišné body, trigonometrie pravého trojúhelníku umožňuje vypočítat skalární součin díky ortogonální projekci . Ve skutečnosti, pokud $H$ je ortogonální projekce $C$ na přímku $( AB )$ , skalární součin je pak v absolutní hodnotě rovný součinu vzdáleností $AH$ a $AB$ . Pokud je $A$ mezi $H$ a $B$ , je tečkový součin jinak záporný a kladný. Všimli jsme si, že pokud je $H$ zaměňováno s $A$ , pak je skalární součin nulový.

${\ displaystyle {\ overrightarrow {AB}} \ cdot {\ overrightarrow {AC}} = {\ overline {AB}} \ times {\ overline {AH}} = AB \ krát AH}$

${\ displaystyle {\ overrightarrow {AB}} \ cdot {\ overrightarrow {AC}} = {\ overline {AB}} \ times {\ overline {AH}} = - AB \ krát AH}$

Tečkový součin se někdy v této formě používá k určení práce síly během posunutí: práce síly F podél dráhy u je bodovým součinem dvou vektorů. Na druhém obrázku se tato práce rovná $- AB \times AH$ .

Kosinový zákon

Existuje obecnější způsob vyjádření Pythagorovy věty známý pod jmény Al-Kashiho věty (ve Francii) nebo generalizované Pythagorovy věty . Zabývá se případem libovolného trojúhelníku. Se zápisy na obrázku vpravo je tento výsledek, nazývaný zákon kosinů, vyjádřen následovně:

c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos \ gamma \,

nebo znovu .

\ quad ab \ cos \ gamma = {\ dfrac 12} \ vlevo (a ^ {2} + b ^ {2} -c ^ {2} \ vpravo)

Demonstraci najdete v podrobném článku. Tento výsledek je vyjádřen jako skalární součin:

Kosinový zákon - Nechť $A$ , $B$ a $C jsou$ libovolné tři body, pak vždy platí následující vzorec:

\ overrightarrow {AB} \ cdot \ overrightarrow {AC} = {\ dfrac 12} \ vlevo ({\ overrightarrow {AB}} ^ {2} + {\ overrightarrow {AC}} ^ {2} - {\ overrightarrow {BC }} ^ {2} \ vpravo)

Obecnější povaha této formulace umožňuje vysvětlit a jednoduše předvést algebraické vlastnosti skalárního součinu. Střední věta je speciální případ.

Dotový produkt jako oblast

Vyjádření kosinového zákona tečkovým produktem naznačuje formulaci tečkového produktu z hlediska plochy. Skalární součin pomocí označení odstavce na projektu odpovídá ploše základního obdélníku $AH$ a výšce $AB$ .

Zvažte bodový součin v orientované rovině, od $x$ do $y$ na obrázku vpravo. Skalární součin vektorů $x$ a $y$ se rovná orientované oblasti paralelogramu konstruovány díky vektory $y$ a $x r$ . Vektor $x r$ je obraz vektoru $x$ přímou rotací v pravém úhlu. Tento přístup je Peano . K tomu používá nástroj s názvem determinant a používá následující formulaci tečkového produktu, geometrickou konstrukcí, ekvivalentní s článkem:

{\ displaystyle x \ cdot y = \ det (y, x_ {r})}

Ve výkresu byly paralelogramy deformovány do obdélníků stejné oblasti pomocí smykové vlastnosti. Zelená plocha je produkt s kladnou tečkou a růžová s produktem se zápornou tečkou.

Tato geometrická forma má určitou výhodu, umožňuje stanovit algebraické vlastnosti skalárního součinu. Tyto vlastnosti jsou užitečné jak pro stanovení analytického výrazu užitečného pro řešení mnoha problémů, tak pro stanovení nové formulace, která je obecnější a provoznější.

Ortogonalita, kolineárnost a úhel

Takové definice bodového součinu poskytují zajímavé nástroje pro kontrolu ortogonality , kolinearity nebo určení geometrického úhlu.

Ortogonalita : vektory a jsou ortogonální, pokud je jeden z vektorů nulový nebo pokud je geometrický úhel $AOB$ správný. Pokud jde o bodový součin, výsledkem je pouze jedna podmínka a jsou ortogonální právě tehdy . $\ overrightarrow {OA}$ $\ overrightarrow {OB}$ $\ overrightarrow {OA}$ $\ overrightarrow {OB}$ ${\ displaystyle {\ overrightarrow {OA}} \ cdot {\ overrightarrow {OB}} = 0}$

Kollinearita : vektory a jsou kolineární právě tehdy, jsou-li body $O$ , $A$ a $B$ na stejné přímce. Pokud jde o bodový produkt, znamená to a jsou kolineární, pokud a pouze pokud . Tato definice také zní takto: dva vektory jsou kolineární, pokud je absolutní hodnota jejich tečkového součinu rovna součinu jejich délek. $\ overrightarrow {OA}$ $\ overrightarrow {OB}$ $\ overrightarrow {OA}$ $\ overrightarrow {OB}$ $| \ overrightarrow {OA} \ cdot \ overrightarrow {OB} | = OA \ krát OB$

Geometrický úhel : pokud a jsou dva nenulové vektory, geometrický úhel je určen rovností . $\ overrightarrow {OA}$ $\ overrightarrow {OB}$ $\ widehat {AOB}$ $\ cos (\ widehat {AOB}) = {\ dfrac {\ overrightarrow {OA} \ cdot \ overrightarrow {OB}} {OA \ krát OB}}$

Algebraické vlastnosti

Pro zjednodušení se používají jiné notace. Vektory nejsou označovány jako dvoubodové, ale pouze jako písmeno . Skalární součin se pak vždy zaznamená o jeden bod . Stává se také, že vektory jsou zaznamenány bez šipek; aby nedocházelo k záměně mezi součinem skaláru vektorem a skalárním součinem mezi dvěma vektory, je skalární součin označen ( u , v ) nebo jinak . Konvence, která se ne vždy dodržuje, spočívá ve výběru řeckých písmen pro skaláry, což umožňuje zabránit nejasnostem. Ve zbytku článku následuje konvence vektoru převyšovaného šipkou a skalárního součinu označeného bodem. $\ overrightarrow {AB}$ ${\ vec v}$ ${\ displaystyle {\ vec {u}} \ cdot {\ vec {v}}}$ $\ left \ langle u | v \ right \ rangle$

Termín skalární součin naznačuje existenci operace, která se dvěma vektory spojuje skalární. Ve vektorovém prostoru jsou skaláry koeficienty, kterými máme právo vynásobit vektory. V elementárním přístupu jsou tyto skaláry skutečné. Skutečnost, že se tato operace nazývá produktem, naznačuje existenci vlastností, které člověk obvykle od produktu očekává (komutativita, distribučnost s ohledem na sčítání ...).

Symetrie

Symetrie je vlastnost, která se vztahuje na funkce dvou proměnných odebraných ze stejné sady. Vzhledem k tomu, soubor S a funkce f definovaný v E x e . Říká se, že je symetrický, právě když:

\ forall (x, y) \ v E ^ {2} \ quad f (x, y) = f (y, x)

Rámec této definice je tvořen tečkovým součinem, který spojuje číslo se dvěma vektory.

Protože délka segmentu [ B , C ] odpovídá délce segmentu [ C , B ], Al-Kashiho věta stanoví symetrii tečkového součinu:

Symetrie bodového součinu - Bodový součin definovaný ve vektorovém prostoru E je symetrický, tj. Vždy platí následující věta:

\ forall ({\ vec x}, {\ vec y}) \ v E ^ {2} \ quad {\ vec x} \ cdot {\ vec y} = {\ vec y} \ cdot {\ vec x}

Bilinearita

Tečkový produkt ve vektorovém prostoru E je správně kompatibilní s přidáním. Tato vlastnost znamená, že bodový produkt vektoru součtem dvou vektorů se rovná součtu dvou bodových produktů:

{\ displaystyle \ forall \ left ({\ vec {x}}, {\ vec {y}}, {\ vec {y}} '\ right) \ v E ^ {3} \ quad {\ vec {x} } \ cdot \ left ({\ vec {y}} + {\ vec {y}} '\ doprava) = {\ vec {x}} \ cdot {\ vec {y}} + {\ vec {x}} \ cdot {\ vec {y}} '}

Tuto kompatibilitu ilustruje obrázek vlevo (kde ). Je to důsledek skutečnosti, že překlad opouští oblast povrchu neměnnou. Aplikace tohoto druhu, takže úhly, délky a v důsledku toho se povrchy neměnný, se nazývá isometry . Každý ze dvou obdélníků šrafovaných zeleně má pro oblast tečkový součin s , červený obdélník má pro oblast tečkovaný součin s . Součet těchto dvou oblastí se skutečně rovná ploše barevného obdélníku (červené a růžové), který je součinem bodu s . Překlad skutečně ponechává povrch neměnný. Požadovaná rovnost je dobře ověřena. ${\ displaystyle {\ vec {y_ {1}}} = {\ vec {y_ {2}}} = {\ vec {y}}}$ $\ vec x$ $\ vec y$ $\ vec x$ ${\ displaystyle {\ vec {y}} '}$ $\ vec x$ ${\ displaystyle {\ vec {y}} + {\ vec {y}} '}$

Symetrie bodového produktu a také kompatibilita vpravo ukazuje kompatibilitu nalevo od přidání:

{\ displaystyle \ forall \ left ({\ vec {x}}, {\ vec {x}} ', {\ vec {y}} \ right) \ v E ^ {3} \ quad \ left ({\ vec {x}} + {\ vec {x}} '\ doprava) \ cdot {\ vec {y}} = {\ vec {x}} \ cdot {\ vec {y}} + {\ vec {x}} '\ cdot {\ vec {y}}}

Je také možné hovořit o kompatibilitě vpravo pro produkt pomocí skaláru. Tato vlastnost má následující podobu:

{\ displaystyle \ forall \ left ({\ vec {x}}, {\ vec {y}} \ right) \ v E ^ {2} \; \ forall \ lambda \ in \ mathbb {R} \ quad {\ vec {x}} \ cdot \ left (\ lambda {\ vec {y}} \ right) = \ lambda \ left ({\ vec {x}} \ cdot {\ vec {y}} \ right)}

Bod zde označuje jak násobení skalárním, tak skalárním součinem. Použití šipek k označení vektorů i řeckých písmen k označení čísel pomáhá předcházet nejednoznačnosti.

Tato kompatibilita je důsledkem Thalesovy věty . Obrázek vpravo ilustruje tuto vlastnost. Fialový obdélník má výšku rovnou výšce zeleného trojúhelníku a jeho základna se rovná OD . Dva trojúhelníky OAB a OCD jsou podobné, proto je možné použít Thalesovu větu, která ukazuje, že jako OC = λ ⋅ OA , pak OD = λ ⋅ OB . Jeho povrch je tedy dobře vynásoben λ .

Stejně jako dříve je důsledkem symetrie kompatibilita vlevo:

{\ displaystyle \ forall \ left ({\ vec {x}}, {\ vec {y}} \ right) \ in E ^ {2} \; \ forall \ lambda \ in \ mathbb {R} \ quad \ left (\ lambda {\ vec {x}} \ vpravo) \ cdot {\ vec {y}} = \ lambda \ doleva ({\ vec {x}} \ cdot {\ vec {y}} \ doprava)}

Aplikace tedy pro jednu, která spojuje číslo s vektorem, splňuje následující vlastnost: $\ vec x$ $\ vec y$ ${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}}}$

{\ displaystyle \ forall \ left ({\ vec {x}}, {\ vec {y}}, {\ vec {y}} '\ right) \ v E ^ {3} \ quad \ forall \ left (\ lambda, \ lambda '\ right) \ in \ mathbb {R} ^ {2} \ quad {\ vec {x}} \ cdot \ left (\ lambda {\ vec {y}} + \ lambda' {\ vec { y}} '\ right) = \ lambda \ left ({\ vec {x}} \ cdot {\ vec {y}} \ right) + \ lambda' \ left ({\ vec {x}} \ cdot {\ vec {y}} '\ right)}

Potom řekneme, že skalární součinová aplikace je lineární vpravo , podobně lineární je vlevo . O takové aplikaci se říká, že je bilineární . Aplikace má čísla jako hodnoty, takže mluvíme o tvaru .

Tečkový produkt je bilineární forma .

Pozitivní určitý charakter

Tečkový součin vektoru se sebou samým se rovná ploše čtverce kromě délky jednoho z jeho zástupců. Výsledkem je, že bodový součin vektoru je sám o sobě vždy pozitivní. Tato hodnota je nula právě tehdy, když je vektor nulový, protože pouze nulový vektor má zástupce nulové délky. Dedukujeme následující definice a tvrzení:

říká se symetrická bilineární forma : (⋅∣⋅){\ displaystyle (\ cdot \ mid \ cdot)} ${\ displaystyle (\ cdot \ mid \ cdot)}$
- definovány v případě , ${\ displaystyle (x \ mid x) = 0 \ Rightarrow x = 0}$
- Pozitivní -li , ${\ displaystyle \ forall x \ in E \ quad (x \ mid x) \ geq 0}$
- pozitivní definitivní, pokud je to obojí, tj. pokud pro jakýkoli nenulový vektor x je obraz ( x , x ) přísně pozitivní;
tečkovaný produkt je pozitivní definitivní forma.

Jakákoli určitá forma je zjevně nedegenerovaná , tj. že pro takový tvar je jediným vektorem kolmým na celý prostor nulový vektor. Opak platí pro pozitivní formy, proto „pozitivní určitý“ je ekvivalentní „nedegenerovanému pozitivnímu“.

Rozvaha: skutečný bodový produkt

Tečkový produkt je pozitivní definitivní symetrická bilineární forma nad vektorovým prostorem nad reálnými čísly.

Algebraické vlastnosti pozorované v případě dimenze 2 nebo 3 jsou dostatečné k definování produktu bodu v jakémkoli reálném vektorovém prostoru.

Nechť $E$ je skutečný vektorový prostor.

Říkáme, že aplikace

{\ displaystyle {\ begin {array} {llcl} (~ \ mid ~): & E \ times E & \ rightarrow & \ mathbb {R} \\ & (x, y) & \ mapsto & (x \ mid y ) \ end {pole}}}

je bodový produkt, pokud je:

bilineární :je lineární vzhledem ke každému argumentu (druhý je pevný); ${\ displaystyle (~ \ mid ~)}$
symetrické : ; ${\ displaystyle \ forall (x, y) \ v E ^ {2} \ quad (y \ mid x) = (x \ mid y)}$
pozitivně definitní :. ${\ displaystyle \ forall x \ in E \ setminus \ {0 \} \ quad (x \ mid x)> 0}$

Je přirozené položit si vzájemnou otázku: je možné definovat geometrii pomocí vektorového prostoru a skalárního součinu? Délka je pak dána normou a úhlem θ mezi dvěma nenulovými vektory a vzorcem: $\ vec x$ $\ vec y$

{\ displaystyle \ theta = \ arccos \ left ({\ dfrac {{\ vec {x}} \ cdot {\ vec {y}}} {\ | {\ vec {x}} \ | \ times \ | {\ vec {y}} \ |}} \ vpravo).}

Taková geometrie uspokojuje trojúhelníkové a Cauchy-Schwarzovy nerovnosti a věty Thales a Pythagoras .

Euklidovský prostor

Euklidovský prostor je vektorový prostor na ℝ, konečné dimenze a opatřený skalárním součinem.

Takový prostor má mnoho vlastností, které jsou algebraické i geometrické. Produkt tečka zvýrazňuje konkrétní lineární aplikace s více vlastnostmi. Umožňují mimo jiné definovat mnoho dalších struktur, často také euklidovských. Nabízí geometrický rámec, který umožňuje zobecnit velký počet skutečných výsledků na reálná čísla. To umožňuje aplikovat výsledky skutečné analýzy na diferenciální geometrii .

Analytické vyjádření

Ortonormální základ

V konečném dimenzionálním vektorovém prostoru umožňují algebraické vlastnosti vyjádřit bodový produkt pomocí souřadnicového systému. Výraz je zjednodušený, když je zvolený základ ortonormální (základní vektory mají normu rovnou 1 a jsou ortogonální dva po dvou).

Například, volbou ( , , ) orthonormal základ v R3, v případě, že dva vektory a mají příslušné souřadnice ( x 1 , x 2 , x 3 ) a ( Y 1 , Y 2 , Y 3 ) získáme vzorec: ${\ vec {e_ {1}}}$ ${\ vec {e_ {2}}}$ ${\ vec {e_ {3}}}$ $\ vec x$ $\ vec y$

${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = x_ {1} y_ {1} + x_ {2} y_ {2} + x_ {3} y_ {3}}$ .

Vyplývá to z vývoje skalárního součinu dvou vektorů vyjádřených v bázi:

${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = (x_ {1} {\ vec {e_ {1}}} + x_ {2} {\ vec {e_ {2}}} + x_ {3} {\ vec {e_ {3}}}) \ cdot (y_ {1} {\ vec {e_ {1}}} + y_ {2} {\ vec {e_ {2}}} + y_ {3} {\ vec {e_ {3}}}),}$

který je vlastnostmi bilinearity a symetrie zapsán:

${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = x_ {1} y_ {1} \, {\ vec {e_ {1}}} \ cdot {\ vec {e_ {1} }} + x_ {2} y_ {2} \, {\ vec {e_ {2}}} \ cdot {\ vec {e_ {2}}} + x_ {3} y_ {3} \, {\ vec { e_ {3}}} \ cdot {\ vec {e_ {3}}} + (x_ {1} y_ {2} + x_ {2} y_ {1}) {\ vec {e_ {1}}} \ cdot {\ vec {e_ {2}}} + (x_ {1} y_ {3} + x_ {3} y_ {1}) {\ vec {e_ {1}}} \ cdot {\ vec {e_ {3} }} + (x_ {2} y_ {3} + x_ {3} y_ {2}) {\ vec {e_ {2}}} \ cdot {\ vec {e_ {3}}},}$

s pro všechny i , a pro všechny i odlišný od j , . ${\ displaystyle {\ vec {e_ {i}}} \ cdot {\ vec {e_ {i}}} = 1}$ ${\ displaystyle {\ vec {e_ {i}}} \ cdot {\ vec {e_ {j}}} = 0}$

Matrix psaní

Na ortonormální bázi existuje jednoduchý způsob, jak vyjádřit bodový produkt pomocí matic. Dva vektory a předchozí odstavec mají následující podobu: $\ vec x$ $\ vec y$

{\ displaystyle {\ vec {x}} \ leftrightarrow X = {\ begin {pmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \ end {pmatrix}}, \ qquad {\ vec {y }} \ leftrightarrow Y = {\ begin {pmatrix} y_ {1} \\ y_ {2} \\ y_ {3} \ end {pmatrix}}}

Matice X a Y představují dva vektory. Pomocí transponované operace a násobení matic získáme rovnost:

\ vec x \ cdot \ vec y = {} ^ tX ~ Y = \ begin {pmatrix} x_1 & x_2 & x_3 \ end {pmatrix} \ begin {pmatrix} y_1 \\ y_2 \\ y_3 \ end {pmatrix} = x_1 y_1 + x_2 y_2 + x_3 y_3

Jakákoli základna

Pokud je báze vybrána libovolně, je vyjádření skalárního součinu složitější. Označme $($ $φ$ $1$ $,$ $φ$ $2$ $,$ $φ$ $3$ $)$ a $($ $ψ$ $1$ $,$ $ψ$ $2$ $,$ $ψ$ $3$ $)$ souřadnice vektorů a na tomto novém základě. Pak máme rovnost: ${\ displaystyle \ left ({\ vec {b_ {1}}}, {\ vec {b_ {2}}}, {\ vec {b_ {3}}} \ doprava)}$ $\ vec x$ $\ vec y$

{\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = {} ^ {t} \ Phi ~ M ~ \ Psi \ quad {\ text {with}} \ quad}

{\ displaystyle {\ vec {x}} \ leftrightarrow \ Phi = {\ begin {pmatrix} \ varphi _ {1} \\\ varphi _ {2} \\\ varphi _ {3} \ end {pmatrix}}, \ quad {\ vec {y}} \ leftrightarrow \ Psi = {\ begin {pmatrix} \ psi _ {1} \\\ psi _ {2} \\\ psi _ {3} \ end {pmatrix}}, \ quad M = {\ begin {pmatrix} {\ vec {b_ {1}}} \ cdot {\ vec {b_ {1}}} & {\ vec {b_ {1}}} \ cdot {\ vec {b_ { 2}}} & {\ vec {b_ {1}}} \ cdot {\ vec {b_ {3}}} \\ [5pt] {\ vec {b_ {2}}} \ cdot {\ vec {b_ { 1}}} & {\ vec {b_ {2}}} \ cdot {\ vec {b_ {2}}} & {\ vec {b_ {2}}} \ cdot {\ vec {b_ {3}}} \\ [5pt] {\ vec {b_ {3}}} \ cdot {\ vec {b_ {1}}} a {\ vec {b_ {3}}} \ cdot {\ vec {b_ {2}}} & {\ vec {b_ {3}}} \ cdot {\ vec {b_ {3}}} \ konec {pmatrix}}}

Matice M se v základu nazývá Gramova matice tečkového produktu . Má mnoho vlastností: je skutečně symetrický, a proto jej lze diagonalizovat ; jeho vlastní čísla jsou navíc přísně pozitivní. O takové matici se říká, že je pozitivně definitivní . ${\ displaystyle \ left ({\ vec {b_ {1}}}, {\ vec {b_ {2}}}, {\ vec {b_ {3}}} \ doprava)}$

Na základě fixního reálného vektorového prostoru E dimenze n definujeme touto metodou bijekci mezi skalárními součiny na E a skutečnými symetrickými pozitivními určitými maticemi velikosti n .

Zobecnění na složité vektorové prostory

Produkt Hermitian Dot

Abychom přizpůsobili definici skutečného skalárního součinu složitým vektorovým prostorům, potřebujeme pojem „semi-linearita“:

Mapa f komplexního vektorového prostoru E v ℂ se říká, že semi-lineární , pokud splňuje:

$\ forall (x, y) \ v E ^ {2} \ quad f (x + y) = f (x) + f (y)$
${\ displaystyle \ forall x \ in E, \ forall \ lambda \ in \ mathbb {C} \ quad f (\ lambda x) = {\ overline {\ lambda}} f (x).}$

Nechť tedy E je komplexní vektorový prostor.

Říkáme, že aplikace : ${\ displaystyle (~ \ mid ~)}$

{\ displaystyle E \ krát E \ to \ mathbb {C}}

(x, y) \ mapsto (x | y)

je levý hermitovský bodový produkt (nebo jen bodový produkt ), pokud je:

sesquilinear vlevo : to znamená

lineární vzhledem k druhému argumentu (první je opravený)

(x | \ mu y) = \ mu (x | y)

semi-lineární vzhledem k prvnímu argumentu (druhý je opravený)

(\ lambda x | y) = \ overline {\ lambda} (x | y)

;

Hermitian symetrické : ; $\ forall (x, y) \ v E ^ {2} \ quad (y | x) = \ overline {(x | y)}$
Pozitivní : ; ${\ displaystyle \ forall x \ in E \ quad (x | x) \ in \ mathbb {R} _ {+}}$
definovány : . ${\ displaystyle (x | x) = 0 \ Rightarrow x = 0}$

Poznámka : konvence linearity vpravo, semi-linearita vlevo není univerzální, někteří autoři používají obrácenou konvenci. V komplexním vektorovém prostoru, který je vybaven takovým tečkovým součinem, se stále ověřuje Pythagorova věta , Cauchy-Schwarzova nerovnost a trojúhelníková nerovnost .

Prehilbertian prostor

Prehilbertovský prostor je skutečný nebo složitý vektorový prostor, obvykle nekonečné dimenze, který jsme poskytli se skalárním součinem. Definice skalárního součinu poté opouští pole tradiční geometrie.

Příklady

V prostoru ℝ n , budeme definovat kanonické skalární součin : . ${\ big (} (x_ {1}, ..., x_ {n}) | (y_ {1}, ..., y_ {n}) {\ big)} = x_ {1} y_ {1} + \ cdots + x_ {n} y_ {n}$
V ℂ prostor n definujeme kanonické skalární součin: . ${\ displaystyle {\ big (} (z_ {1}, ..., z_ {n}) | (w_ {1}, ..., w_ {n}) {\ big)} = {\ overline {z_ {1}}} w_ {1} + \ cdots + {\ overline {z_ {n}}} w_ {n}}$
Nechť E je ℝ-vektorový prostor spojitých funkcí intervalu $[ a , b ]$ v ℝ.

Aplikace je skalární součin na E .

{\ displaystyle E \ times E \ to \ mathbb {R}, (f, \, g) \ mapsto \ int f \ times g}

Nechť F je ℂ-vektorový prostor spojitých funkcí intervalu $[ a , b ]$ v ℂ.

Použití: je skalární součin na F .

{\ displaystyle F \ times F \ rightarrow \ mathbb {C}, (f, g) \ mapsto \ int {\ overline {f}} \ krát g}

Poznámka: Pokud namísto práce na spojitých funkcích pracujeme na spojitých funkcích po částech , vytvořená bilineární forma je skutečně pozitivní, ale není definována: ( f | f ) = 0 znamená, že f je nula s výjimkou jejích bodů diskontinuity .

Poustevnický prostor

Hermitovský prostor je vektorový prostor definovaný na komplexních číslech, konečné dimenze, který má hermitovský součin, což odpovídá zobecnění skutečného případu. V této souvislosti se také používá výraz dot product. Výsledky a vlastnosti euklidovských prostorů jsou často jednoduše přeloženy do tohoto prostoru.

Hilbertův prostor

Hilbertův prostor může být skutečný nebo složitý. Přesně odpovídá dvěma předchozím případům s tím rozdílem, že dimenze nemusí být nutně konečná. Pokud se teorie a důkazy liší od konečné dimenzionální situace, některé výsledky se zobecní. Předpokladem je však často nezbytné, aby v úplnosti na přidružené metrickém prostoru . Z tohoto důvodu je Hilbertův prostor podle definice úplný.

Tento prostor se používá k řešení problémů funkční analýzy , zejména parciálních diferenciálních rovnic .

Poznámky a odkazy

Cílem tohoto článku je následovat tento přístup, pro technickou prezentaci viz „ Prehilbertianův prostor “ nebo „ Euklidovský prostor “.
(od) HG Grassmann (1847), Geometrische Analyze , Lipsko.
(in) S. Dolecki a GH Greco, „ K historickým kořenům nezbytných podmínek optimality - Regula of Peano “ , Control and Cybernetics , sv. 36,2007, str. 491-518.
Podle webové stránky (v) „ Nejstarší známá použití Matematických recenzí některá slova ' .

Podívejte se také

Související články

Externí odkaz

Rudolf Bkouche , „ Odkud pochází tečkovaný produkt? » , Na kultuře