Plástev

Buňky (nebo buňky), konstruovány tak, aby 90% vosku a 10% pylu a propolisu od včel pracovníkům v této oblasti budou úlu v medu je pyl nebo plod (vajíčka a larvy) jsou hranoly vedle sebe s vodorovnými osami, které tvoří voskový dort. Tento voskový koláč nebo paprsek je tedy vytvořen ze dvou řad šestiúhelníkových buněk, které se setkávají na jejich základně, která se skládá ze tří zkosených ploch.

Co je ale opravdu překvapivé, je více než singulární tvar těchto buněk. Druhý konec těchto buněk není obyčejný šestiúhelník, ale blokování tří identických diamantů, nazývaných kosodélníky . Hranoly proto nejsou spojeny svým šestihranným povrchem, ale právě těmito diamanty, přičemž každá buňka je pomocí těchto povrchů zálohována, odsazena, ke třem dalším.

Buňky jsou stavěny od poloviny března do poloviny července (na severní polokouli) voskovými včelami. Konstrukce buňky začíná ve spodní části. Tloušťka stěny je malá (méně než 300 mikrometrů, je průsvitně průsvitná), pouze horní okraj je silnější, aby se nerozpadl.

Rozměry

Viditelnou částí každé z buněk je pravidelný šestiúhelník, jehož strana měří přibližně 3  mm . Hloubka buňky je 11,5  mm . Tloušťka jeho stěn je asi dvacátá milimetr. Každá buňka je zálohována třemi dalšími buňkami pomocí povrchu tvořeného třemi diamanty (kosočtverci).

Buňky nejsou umístěny dokonale vodorovně. Vytvářejí úhel 7 až 8 stupňů nahoru, aby se zabránilo medu vytékat ven z buněk ( kapilarita ).

Včely samy spontánně vytvářejí buňky o průměru asi 5  mm (proměnlivé rozměry v závislosti na odrůdách včel a umístění buněk, tj. 4,8  mm pro plodové buňky a 5,3  mm pro medové buňky), ale tyto komerčně dostupné embosované vosky měří 5,4 na 5,7  mm .

Každý rám těla úlu Dadant má vnitřní rozměry 41 × 26,5  cm . Má tedy maximální teoretickou kapacitu 82 × 53 = 4346 buněk o šířce 5  mm na stranu, tj. 8692 na snímek, ale rámy jsou zřídka úplně a dokonale sestavené, v průměru je 3500 buněk na stranu, a tedy 7000 po rámech ( a o polovinu méně pro rámec zvýšení).

Vnitřní objem plicních sklípků se zmenšuje, protože tam dochází k více porodům. Z tohoto důvodu a ze zdravotních důvodů se doporučuje neudržovat zastavěné prostředí déle než pět let (v průběhu času ztmavne, což je známkou toho, že je nutné jej vyměnit).

Historický přehled

Hexagonální tvar buněk byl identifikován Aristotleem z IV th  století  před naším letopočtem. AD ( History of animals ) poté o osm století později geometricky zacházel Pappus, řecký matematik  ; ale to nebylo až do XVIII -tého  století , že tento tvar kosočtverce byl zaznamenán. Tak Maraldi , astronom na pařížské observatoře , experimentálně stanovena v roce 1712 hodnoty úhlů těchto kosočtverců, které se rovnají 109 ° 28 'a 70 ° 32'.

Astronom Johannes Kepler ( zaujatý analogií mezi pravidelností uspořádání alveol a krystalů), zaujatý složitostí těchto forem, předpokládá, že včely mají ve své domněnce z roku 1611 matematické myšlení ) a fyzik Réaumur ve svých pamětech, které mají sloužit historii hmyzu , podezřívá včely, že si kvůli ekonomice staví svůj voskový dort. Aby ověřil svou hypotézu, požádal německý geometr König, aby určil, která je hexagonální buňka se dnem složeným ze tří stejných kosodélníků, které lze postavit z co nejmenšího množství materiálu. König diferenciálním výpočtem v roce 1739 zjistil, že úhly těchto diamantů musí být rovny 109 ° 26 ′ a 70 ° 34 ′. Soulad tohoto výsledku s výsledkem Maraldiho je již udivující, ale v roce 1743 ho vylepšil skotský matematik Maclaurin, který prokázal, že König udělal chybu ve svých výpočtech a že úhly diamantů odpovídající použití minima hmoty byly přesně ty, které naznačil Maraldi: 109 ° 28 ′ a 70 ° 32 ′ [optimální matematické hodnoty se shodují s Arc cos (-1/3) a Arc cos (1/3)]. je to úhel kontaktních ploch 4 mýdlových bublin, které se setkávají v bodě. Mýdlové bubliny vždy díky svému povrchovému napětí dosáhnou minimálního povrchového napětí daného obrysu.

Byl to Réaumur, kdo navrhl původní a avantgardní myšlenku postavit se na stranu šestihranné dlažby jako jednotka měření a velmi lituje, že to nebylo provedeno z měření ve starověkých civilizacích, protože by to poskytlo sledovatelné jednotky opatření.

Na tuto problematiku narazíme: Lhuillier (Berlín, 1781), Lalanne (Ann. Sc. 1840), Brougham (CRAS, 1858) a Hennessy (pro. Roy. Soc. London, 1886), samozřejmě s Buffonem a Guillaume- L. Formanoir de Palteau . Buffon předkládá myšlenku, která se bohužel často opakuje: že současně stlačujeme dvě sady podlouhlých voskových válců; vezmou tento šestihranný tvar. Je to možné, ale včely takto nepostupují: začnou stavěním dna, pak tváří šestihranných válců. Mají tedy v sobě přizpůsobení konstrukci takového reliéfu dna. To jistě vyplývá ze současného oboustranného zhutňování vosku, a Buffonovo vysvětlení tedy nelze opomenout, ale neodpovídá situaci všech buněk dohromady, jak někdy vidíme.

Proč šestiúhelník?

Philip Ball připomíná, že v roce 1660 dánský matematik Rasmus Bartholin navrhl, aby se hexagonální tvar plicních sklípků spontánně vytvořil tlakem vyvíjeným každou včelou na stěny (včely proto neprokázaly talent geodeta), zatímco Charles Darwin měl navrhl v roce 1859, že včely zpočátku postavily kruhovou buňku, která se poté stala šestihrannou.

Prvním zájmem včel je vydláždit plán, aby mohly následně vydláždit prostor. Známe tři pravidelné polygony, které umožňují dláždit rovinu: rovnostranný trojúhelník, čtverec a šestiúhelník. Nyní je možné ukázat, že mezi těmito třemi pravidelnými polygony je pro stejný povrch šestiúhelník pravidelný mnohoúhelník nabízející nejmenší obvod.

Člověk by si však mohl klást otázku, zda je šestiúhelník skutečně dlažbou nejekonomičtějšího letadla. Dalo by se skutečně uvažovat o kombinaci mnohoúhelníků všeho druhu, které nejsou nutně pravidelné nebo dokonce jejichž strany tvoří přímku. Do roku 1943, kdy maďarský matematik László Fejes Tóth prokázal, že pravidelná šestihranná struktura zůstává nejlevnějším polygonem, který připraví rovinu mezi všemi pravostrannými polygony, se o tom nevědělo příliš mnoho . Co se ale stane, když jsou strany zakřivené? Fejes Tóth si myslel, že pravidelná hexagonální struktura zůstane prakticky nejúčinnější, ale ukázal, že existuje další forma umožňující ještě optimálnější využití prostoru a úsporu včel 0,35% vosku.

Teprve v roce 1999 představil Thomas Hales svůj důkaz na 19 stranách ( Honeycomb Theorem ).

V roce 2013 profesor Bhushan Lal Karihaloo  (en) potvrzuje Darwinův návrh. Ukazuje, že neustálá práce pracovníků ohřívá kruhové voštinové voskové koláče na teplotu 45  ° C , viskoelasticita umožňuje tak jednoduchým stlačením buněk k přechodu z kruhového tvaru do šestiúhelníkového tvaru, jako je například "  Hexatura kruhu  ".

Proč kosočtverce?

Dno tvořené třemi diamanty umožňuje jednoduché podložení buněk. Je dokonce snadné dokázat, že je to ekonomičtější než šestihranné ploché dno, ale je to stále nejekonomičtější způsob?

V roce 1964 Fejes Toth prokázal, že pokud by dno bylo tvořeno dvěma malými šestiúhelníky a dvěma diamanty, místo tří kosočtverců by bylo množství vosku při stejném objemu o 0,35% menší než v případě diamantů .

Výpočet úhlů

Abychom určili úhly kosodélníků minimalizujících povrch, můžeme si již všimnout, že nahrazení šestiúhelníkového dna AB'CD′EF ′ dnem tvořeným 3 kosodélníky úhlopříček AC, CE, EF, nemění objem alveolus. Ve skutečnosti je odstraněný objem přesně stejný jako přidaný objem.

Nyní jde o srovnání povrchů.

V kosodélníkovém pozadí je povrchem povrch tří diamantů SABC, SCDE, SEFA

Tento povrch přesně nahrazuje povrch šestihranného dna AB'CD′EF ′ a 6 trojúhelníků rovných trojúhelníku AB′B.

Poloha B je optimální, když plocha (SABC) - 2 × plocha (AB′B) je minimální.

Úhlopříčka diamantu se však snadno vypočítá . Pokud nazýváme P středem kosočtverce, pak oblast SABC je . NAVS=na3{\ displaystyle AC = a {\ sqrt {3}}}na3PB{\ displaystyle a {\ sqrt {3}} PB}

Pokud jde o trojúhelník AB′B, obdélník v B ′, jeho plocha je 12na×BB′{\ displaystyle {\ frac {1} {2}} a \ krát BB '}

Kvantitativní oblast (SABC) - 2 × oblast (AB′B) bude proto minimální, pokud je cesta minimální 3PB-BB′{\ displaystyle {\ sqrt {3}} PB-BB '}

Potom jsou možné dvě metody. Jeden je přístupný na střední škole, druhý využívá Fermatův princip .

Úroveň pro střední školy  : nazýváme x délku BB ′, pak jde o minimalizaci množství

F(X)=3na24+X2-X{\ displaystyle f (x) = {\ sqrt {3}} {\ sqrt {{\ frac {a ^ {2}} {4}} + x ^ {2}}} - x} Výpočet derivace vede k F′(X)=3X2na24+X2-1{\ displaystyle f '(x) = {\ sqrt {\ frac {3x ^ {2}} {{\ frac {a ^ {2}} {4}} + x ^ {2}}}} - 1} Jedná se o rostoucí funkci na (protože se zvyšuje), která mizí , tj. Kdy .R+{\ displaystyle \ mathbb {R} +}X↦3XX+na2/4{\ displaystyle X \ mapsto {\ frac {3X} {X + a ^ {2} / 4}}}Xna24+X2=13{\ displaystyle {\ frac {x} {\ sqrt {{\ frac {a ^ {2}} {4}} + x ^ {2}}}} = {\ frac {1} {\ sqrt {3}} }}BB′BP=13{\ displaystyle {\ frac {BB '} {BP}} = {\ frac {1} {\ sqrt {3}}}} Právě pro tento poměr tedy funkce dosahuje svého minima.F{\ displaystyle f \,}

Fermatův princip  : určuje, že cesta je minimální, když je ortogonální, tj. Když . 3PB-BB′{\ displaystyle {\ sqrt {3}} PB-BB '}3PB→PB-B′B→B′B{\ displaystyle {\ sqrt {3}} {\ frac {\ overrightarrow {PB}} {PB}} - {\ frac {\ overrightarrow {B'B}} {B'B}}}BB′→{\ displaystyle {\ overrightarrow {BB '}}}BB′BP=13{\ displaystyle {\ frac {BB '} {BP}} = {\ frac {1} {\ sqrt {3}}}}

Zbývá jen najít úhly kosočtverce. Voláme aθ=NABVS^{\ displaystyle \ theta = {\ widehat {ABC}}}ϕ=SNAB^{\ displaystyle \ phi = {\ widehat {SAB}}}

• V trojúhelníku PB′B máme

BB′BP=13=cos⁡(B′BP^){\ displaystyle {\ frac {BB '} {BP}} = {\ frac {1} {\ sqrt {3}}} = \ cos ({\ widehat {B'BP}})} PB′BP=23=hřích⁡(B′BP^){\ displaystyle {\ frac {PB '} {BP}} = {\ frac {\ sqrt {2}} {\ sqrt {3}}} = \ sin ({\ widehat {B'BP}})} Které dávají BP=32PB′{\ displaystyle BP = {\ frac {\ sqrt {3}} {\ sqrt {2}}} PB '}

• V trojúhelníku APB ′

NAP=3PB′{\ displaystyle AP = {\ sqrt {3}} PB '}

• Takže v diamantu SABC máme
  • PNAPB=2=opálení⁡(θ/2){\ displaystyle {\ frac {PA} {PB}} = {\ sqrt {2}} = \ tan (\ theta / 2)}, Které dávají cos⁡(θ)=1-21+2=-13{\ displaystyle \ cos (\ theta) = {\ frac {1-2} {1 + 2}} = - {\ frac {1} {3}}}
  • PBPNA=12=opálení⁡(ϕ/2){\ displaystyle {\ frac {PB} {PA}} = {\ frac {1} {\ sqrt {2}}} = \ tan (\ phi / 2)}, Které dávajícos⁡(ϕ)=1-1/21+1/2=13{\ displaystyle \ cos (\ phi) = {\ frac {1-1 / 2} {1 + 1/2}} = {\ frac {1} {3}}}

nebo úhly 109 ° 28 ′ a 70 ° 32 ′, jak zjistil Mac Laurin .

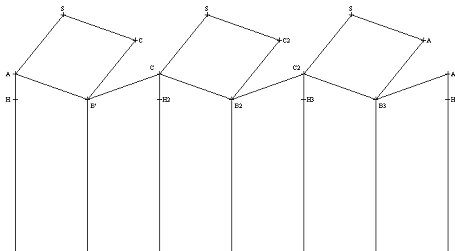
Vývoj včelí buňky

Poznámky a odkazy

1. Vosk a paprsky.
2. Móda nebo nutnost? Návrat do buňky „přirozené“ velikosti (2003) Raymonda Zimmera
3. Ginette Mison, René Gauthier, The bees, the problem of the alveoli , Bulletin de L'APMEP n o  428, str.  403-408 , číst online
4. Aristoteles, Dějiny zvířat , Kniha V, Číst online , str.  303
5. Maraldi, Postřehy o včelách , Monografie Akademie věd, 1712, Číst online , str.  309
6. (in) André Authier, Počátky rentgenové krystalografie , Oxford University Press ,2013( číst online ) , s.  290
7. René Antoine de Réaumur, Paměti k historii hmyzu, svazek 5, 1740, Číst online
8. Jacques Radouan, Auguste Radouan, François Malepeyre, nový kompletní manuál ke správě včel a získávání velkých výhod z nich, svazek 1, Roret, 1860, s. 1.  78
9. Mac Laurin, Na základnách buněk, kde včely ukládají med , Filozofické transakce Královské společnosti v Londýně, 11. července 1743, Číst online
10. Mac Laurin, Na základnách buněk, kde včely ukládají med , Transaction philosophique de la société royale de Londres, 11. července 1743, s.  281
11. René Antoine de Réaumur, Monografie k dějinám hmyzu, svazek 5, 1740, s.  398
12. Lhuillier, Monografie o minimálním vosku včelích plástů včel a zejména o minimálním minimu týkajícím se této záležitosti , Nové monografie Královské akademie v Berlíně, 1781, Číst online
13. Leclerc, Comte de Buffon, Přírodní historie, obecná a konkrétní, s popisem kabinetu Roy, Tome Quatrième, s.  99-100
14. François Huber, Nová pozorování včel , Ženeva, 1814, str.  146
15. (in) Philip Ball, „  Jak se mohou stavět voštiny. Šestiúhelníkové buňky by mohly vytvářet spíše fyzické síly než vynalézavost včel  “ , Nature ,17. července 2013( DOI  10.1038 / nature.2013.13398 )
16. (in) Johannes Kepler, Šestihranná vločka , Paul Dry Books,1966( číst online ) , s.  144
17. (in) Karihaloo BL, Zhang K, Wang J, „  Hřebeny včel: jak se buňky transformují do kruhových zaoblených šestiúhelníků  “ , Journal of the Royal Society. Rozhraní , sv.  10, N O  86,6. září 2013( číst online )

Podívejte se také

Související články

• Kapilarita a mýdlová bublina
• Fermatův princip
• Plástev (struktura)

externí odkazy

• Workshop of APMEP na včel buněk
• Místo na dlažbě