Logistická sada

V matematiky , je logistické sekvence je jednoduché sekvence , ale opakování, která není lineární. Jeho relace opakování je

Xne+1=μXne(1-Xne), X0∈[0;1].{\ displaystyle x_ {n + 1} = \ mu x_ {n} (1-x_ {n}), ~ x_ {0} \ v [0; 1].}

V závislosti na hodnotě parametru μ (v [0; 4], aby x zůstalo v [0; 1]), generuje konvergentní sekvenci, sekvenci vystavenou oscilacím nebo chaotickou sekvenci .

Toto pokračování, které je často uváděno jako příklad složitosti chování, které může vyplynout z jednoduchého nelineárního vztahu, popularizoval biolog Robert May v roce 1976 . Jednou z aplikací logistické sady je modelování velikosti biologické populace po generace.

Jedná se o řešení, v diskrétním čase z Verhulst modelu . Termín „logistika“ vychází z práce Pierra Françoise Verhulsta, který logickou křivku nazývá kontinuálním časovým řešením svého modelu. V roce 1845 napsal ve své práci věnované tomuto jevu: „Dáme této křivce termín logistika“ . Autor nevysvětluje svou volbu, ale „logistika“ má stejný kořen jako logaritmus a logistikos znamená „výpočet“ v řečtině.

Chování podle μ

V logistickém modelu budeme uvažovat, že zde uvedená proměnná x n označuje poměr populace druhu k maximální populaci tohoto druhu (je to číslo mezi 0 a 1). Změnou parametru μ lze pozorovat několik různých chování:

Případ 0 ≤ µ ≤ 1 populace zanikla.

Nakonec druh zemře, bez ohledu na počáteční populaci. Tj . lim+∞Xne=0{\ displaystyle \ lim _ {+ \ infty} x_ {n} = 0}

Případ 1 ≤ µ ≤ 3 velikost populace se stabilizuje.

• Pokud je 1 ≤ µ ≤ 2 , populace se stabilizuje kolem hodnoty , bez ohledu na počáteční populaci. Jinými slovy .μ-1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}lim+∞Xne=μ-1μ{\ displaystyle \ lim _ {+ \ infty} x_ {n} = {\ frac {\ mu -1} {\ mu}}}
• Pokud 2 ≤ µ ≤ 3 , také se po určité době osciluje a stabilizuje . Rychlost konvergence je lineární, s výjimkou µ = 3, kde je velmi pomalá.μ-1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}

Případ 3 ≤ µ ≤ 3,57 velikost populace osciluje mezi 2, 4, 8… hodnotami (síla 2).

• Pokud 3 <µ ≤ 1 + √6 (asi 3,45), skončí oscilováním mezi dvěma hodnotami, v závislosti na µ, ale ne na počáteční populaci.
• Pokud je 3,45 <µ <3,54 (přibližně), nakonec osciluje mezi čtyřmi hodnotami, opět v závislosti na µ, ale ne na počáteční populaci.
• Pokud je µ o něco větší než 3,54, populace nakonec osciluje mezi osmi hodnotami, pak 16, 32 atd. Interval hodnot µ vedoucí ke stejnému počtu kmitů rychle klesá. Poměr mezi dvěma po sobě jdoucími intervaly se blíží pokaždé Feigenbaumově konstantě , δ = 4 669…. Žádné z těchto chování nezávisí na počáteční populaci.

Případ 3.57 ≤ µ velikost populace je až na výjimky chaotická .

• Kolem μ = 3,57 , chaos sady v. Dosud není viditelná žádná oscilace a mírné rozdíly v počáteční populaci vedou k radikálně odlišným výsledkům.
• Většina hodnot nad 3,57 vykazuje chaotický charakter, ale existuje několik izolovaných hodnot µ s chováním, které není. Například od 1 + √8 (asi 3,82) malý interval hodnot µ vykazuje oscilaci mezi třemi hodnotami a pro µ o něco větší, mezi šesti hodnotami, pak dvanácti atd. Jiné intervaly nabízejí oscilace mezi 5 hodnotami atd. Jsou přítomna všechna oscilační období, opět nezávisle na počáteční populaci.
• Za µ = 4 poměr populace druhu k maximální populaci opouští interval [0,1] a odchyluje se téměř pro všechny počáteční hodnoty.

Výše popsané oscilační periody splňují následující pravidlo. Zvažte Charkovského pořadí definované na přísně pozitivních celých číslech takto:

3◃5◃7◃...◃2×3◃2×5◃2×7◃...◃2ne×3◃2ne×5◃2ne×7◃...{\ Displaystyle 3 \; \ triangleleft \; 5 \; \ triangleleft \; 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 \ krát 3 \; \ triangleleft \; 2 \ krát 5 \; \ triangleleft \; 2 \ krát 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \ krát 3 \; \ triangleleft \; 2 ^ {n} \ krát 5 \; \ triangleleft \; 2 ^ {n} \ krát 7 \; \ triangleleft \; \ ldots} ◃2ne+1×3◃2ne+1×5◃...◃2ne◃2ne-1◃...◃22◃2◃1{\ displaystyle \; \ triangleleft \; 2 ^ {n + 1} \ krát 3 \; \ triangleleft \; 2 ^ {n + 1} \ krát 5 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \; \ triangleleft \; 2 ^ {n-1} \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {2} \; \ triangleleft \; 2 \; \ triangleleft \; 1 } Jinými slovy, nejdříve umístíme liché začínající od 3 ve vzestupném pořadí, poté liché vynásobíme 2, poté 4 atd. a končíme s mocninami 2 v sestupném pořadí. Pokud hodnota parametru µ odpovídá periodě oscilace n , pak všechna celá čísla následující n v Charkovského pořadí odpovídají periodám oscilace, které se již objevily u hodnot parametru menších než µ . Jelikož tedy µ = 3,82 odpovídá periodě 3, všechny možné periody oscilace se již objevily u hodnot µ mezi 0 a 3,82.

Bifurkace schéma  (v), použitý k graficky shrnuty různé případy:

Komentáře

Několik jednoduchých úvah a několik grafů částečně osvětlilo výše uvedené výsledky.

Grafika

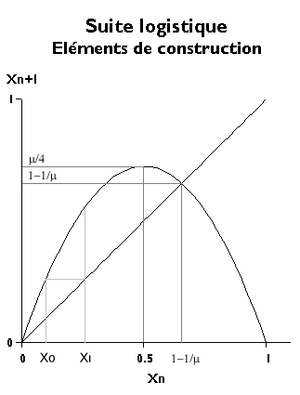
Vývoj logistické posloupnosti lze znázornit v rovině ( x n , x n +1 ).

Základní rovnice představuje parabolu, která prochází body úsečky 0 a 1 na vodorovné ose. Aby hodnoty x n +1 nezůstaly záporné, je nutné zachovat pouze oblouk zahrnutý mezi těmito dvěma body; toto představuje pro x n = 1 ⁄ 2 maximum hodnoty μ ⁄ 4 . Tato hodnota musí být také mezi 0 a 1, proto μ <4.

Pokud posloupnost konverguje, její limit splňuje rovnici lim x n +1 = lim x n . Tato možná hranice, označená x , je řešením kvadratické rovnice

X=μX(1-X){\ displaystyle x = \ mu x (1-x)}

a může tedy nabývat jednu nebo druhou z hodnot

X=0,X=1-1/μ{\ displaystyle x = 0, x = {1- {1 / \ mu}}}

K popisu chování posloupnosti je nutné vycházet z úsečky x 0 , určit na parabole hodnotu x 1, která se poté transformuje do nové úsečky procházející úsečkou x n +1 = x n a tyto dva opakovat operace.

Oblasti konvergence

U určitých hodnot parametru μ se posloupnost chová jako klasická posloupnost a konverguje k jedné ze dvou možných mezí. Základní rovnici lze přepsat ve formě

Xne+1Xne=μ(1-Xne){\ displaystyle {x_ {n + 1} \ přes x_ {n}} = \ mu (1-x_ {n})}

Pokud je posloupnost ohraničena geometrickou posloupností, která má sklon k 0. 0≤μ≤1{\ displaystyle 0 \ leq \ mu \ leq 1}

Chcete-li vidět chování vzhledem k druhému možnému limitu, stačí provést změnu proměnné x n = u n + 1 - 1 / μ. Vzorec se stává:

une+1+1-1/μune+1-1/μ=1-μune{\ displaystyle {{u_ {n + 1} + 1-1 / \ mu} \ nad {u_ {n} + 1-1 / \ mu}} = 1- \ mu u_ {n}}

V tomto případě je stav konvergence vyžaduje, že druhý člen je mezi -1 a +1: . 1≤μ≤3{\ displaystyle 1 \ leq \ mu \ leq 3}

Zkontrolujeme, zda je- li u n blízko limitu 1 - 1 / μ, pak 1-μ u n je blízko 2 - μ a u n má sklon ke své hranici zvyšováním hodnot, pokud je μ menší než 2, o střídavé hodnoty, pokud je větší než 2.

Bifurkace

V předchozím odstavci rekurenční vzorec tvaru x n +1 = f ( x n ) umožnil získat první atraktory hledáním možného limitu v souladu s rovnicí x = f ( x ).

Když je μ větší než 3, musíme hledat řešení rovnice x = f ( f ( x )). To vede k rovnici čtvrtého stupně, která má přirozeně již známé kořeny - ale už nejsou lákadly - a dvojici nových kořenů. 0,1-1μ{\ displaystyle 0,1 - {\ frac {1} {\ mu}}}

12(1+μμ±1μμ2-2μ-3){\ displaystyle {1 \ nad 2} \ vlevo ({1+ \ mu \ nad \ mu} \ pm {1 \ nad \ mu} {\ sqrt {\ mu ^ {2} -2 \ mu -3}} \ že jo)}

Konvergence již neexistuje: objeví se limitní cyklus. Výsledek iterace se střídavě přepíná z jednoho z posledních dvou kořenů na druhý: u n + 1 = u n-1, zatímco u n + 2 = u n . Pro μ = 3,4 se zobrazí postupné přibližné hodnoty 0,84, 0,45, 0,84, 0,45, 0,84 ....

Za hranicí stability tohoto cyklu, √6 + 1, dochází ke dvěma novým bifurkacím, které závisí na řešení x = f (f (f (f (x)))). Pro μ = 3,47 jsou postupné hodnoty řádově 0,47, 0,86, 0,40, 0,84, 0,47 ...

Chaos

Od bifurkace k bifurkaci se vývoj stává stále složitějším. Výsledkem procesu je přibližně μ> 3,57 v systémech, které obecně již nepředstavují viditelné atraktory. Grafika pak představuje „chaotický“ vývoj v obvyklém slova smyslu.

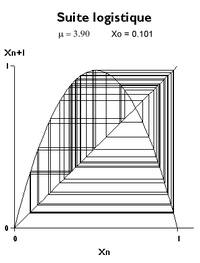
V jazyce matematiků však slovo chaos představuje silnou citlivost na počáteční podmínky. Dva grafy odpovídající μ = 3,9 s počátečními hodnotami u 0 0,100 a 0,101 ukazují, že trajektorie se od sebe vzdalují, dokud se rychle nerozlišují. V konkrétním problému nejsou počáteční podmínky nikdy přesně známy: po určité době se chaotický jev stal nepředvídatelným, i když zákon, který jej definuje, je naprosto deterministický.

Dodatky

Bibliografie

• Alain Hillion , Matematické teorie populací , Paříž, Presses Universitaires de France , kol.  „  Co já vím?  “1986, 127  s. , č. 2258 ( ISBN  2-13-039193-1 )
• Nicolas Bacaër , Dějiny matematiky a populací , Paříž, Éditions Cassini, kol.  "Sůl a železo",2008, 212  s. ( ISBN  978-2-84225-101-7 , upozornění BnF n o  FRBNF42035729 ) , „Verhulst a logistická rovnice“

Související články

• Dynamický systém
• Teorie chaosu
• Ergodická teorie
• Lyapunov fraktál
• Zpětná vazba , samoregulace

externí odkazy

• (en) Elmer G. Wiens, Logistická mapa a chaos
• [PDF] Daniel Perrin, The Logistics Suite and Chaos
• (fr) Interaktivní digitální zážitek z bifurkačního diagramu logistické aplikace http://experiences.math.cnrs.fr

Poznámky a odkazy

1. (in) RM May , „  Jednoduché matematické modely s velmi komplikovanou dynamikou  “ , Nature , sv.  261, n o  55601976, str.  459–467 ( DOI  10.1038 / 261459a0 )
2. (in) Proč ne autokatalytická a logistická křivka hlavice?