Nedělitelná metoda
V geometrii je způsob indivisibles nebo zásada Cavalieri je způsob výpočtu plochy a objemu vynalezený Bonaventura Cavalieri na XVII th století , vyvinutý Gilles de Roberval , Evangelista Torricelli a Blaise Pascal , účinnější než způsob vyčerpání z Archimédova ale také riskantnější použít. Lze jej považovat za předchůdce integrálního počtu , který o něco později vyvinuli Leibniz a Newton .
Princip Cavalieri
Princip je uvedl Liu Hui v III th století a Bonaventura Cavalieri na XVII th století.
Povrch je srovnáním rovnoběžných čar . Pro Cavalieri jsou paralelní čáry segmenty paralelních čar nebo oblouky soustředných kruhů . Každá čára se nazývá nedělitelná oblast, která má být na druhou . Pokud jsou dva povrchy složeny z čar stejné délky, mají stejnou plochu.
Analogický princip existuje pro objemy a stanoví, že objemy dvou objektů jsou stejné, pokud jsou odpovídající průřezy ve všech případech stejné. Dva průřezy se shodují, pokud se jedná o průsečíky objektu s rovinami ve stejné vzdálenosti od dané základní roviny.
Příklady použití
Výpočty plochy
Metoda je velmi efektivní při hledání oblasti disku s poloměrem R a oblasti Archimédovy spirály .
Oblast disku
Disk se skládá ze soustředných kruhů, jejichž délka je 2 π r , kde r se pohybuje od 0 až R . Tyto kruhy jsou nedělitelné části disku.
Základnová trojúhelník L = 2π R a výška R je také složena z délky linie 2n r , kde r je od 0 do R . Tyto segmenty jsou nedělitelné trojúhelníky.
Tyto dva povrchy mají nedělitelné předměty stejné délky, takže mají stejnou plochu. Plocha trojúhelníku je základní x výška / 2 = (2π R x R ) / 2 = π R 2 .
Archimédova spirální oblastArchimédova spirála se získá tím, že pohybuje bod na úsečce s jednotným pohybem, zatímco linie se otáčí kolem bodu s jednotným pohybem. Archimedes bolestně demonstruje, že plocha spirály se rovná jedné třetině plochy disku, který ji obsahuje.
Cavalieri rozřízne spirálu na oblouky, které narovná na segmenty. Princip konstrukce archimédovské spirály umožňuje říci, že má-li oblouk kruhu úhel ve středu t (vyjádřený v radiánech ), je jeho poloměr . Délka oblouku kružnice je proto , kde t je úhel se pohybuje od 0 do 2n .
Narovnané segmenty jsou proto nedělitelné od paraboly se základnou R a výškou π R / 2 . Od Archimeda víme, že plocha takového povrchu se rovná 2/3 obdélníku, který jej obsahuje.
Parabola a spirála jsou tvořeny nedělitelnými prvky stejné délky. Jejich oblasti jsou stejné. Plocha spirály je tedy
Výpočty objemu
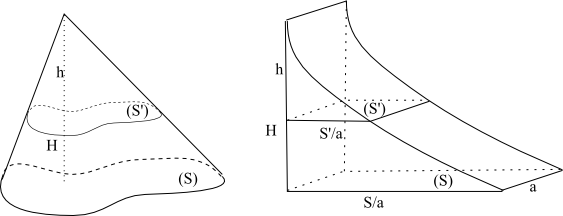
Nedělitelná metoda umožňuje deformaci profilů. Pokud se jejich plocha nezmění, pak těleso a deformované těleso mají stejný objem. Tato metoda je velmi účinná například při demonstraci, že objem kteréhokoli kuželu se rovná jedné třetině objemu válce stejné výšky a stejné základny.
Objem kuželeNa obrázku výše je každá sekce deformována do obdélníku se stejnou oblastí a šířkou a . To zajišťují proporcionální vlastnosti povrchů
Křivka nakreslená ve druhém tělese je tedy parabola. Druhé těleso je válec základny křivočarého trojúhelníku a výšky a . Z Galileo víme, že plocha tohoto křivočarého trojúhelníku se rovná . Zde je tedy oblast křivočarého trojúhelníku . Objem pravého válce (tedy levého kuželu) je tedy .
Objem koule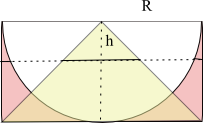
Torricelli pomocí podobných metod opět ukazuje, že objem mísy je stejný jako objem rotačního kužele . Mísa se získá otočením obdélníku o rozměru 2 R × R , zbaveného polodisku o poloměru R , kolem jeho nejmenšího mediánu. Kužel se získá otáčením rovnoramenného pravoúhlého trojúhelníku strany R kolem jedné strany pravého úhlu.
Torricelli ukazuje, že části mísy (růžové) a kuželu (žluté) mají stejnou oblast ve vzdálenosti h od horní části kužele.
Průřez kužele je disk o poloměru h, proto kužel S = π h 2 . Část mísy je korunou o poloměrech R, a proto S bol = π R 2 - π ( R 2 - h 2 ) = π h 2 .Sekce, které mají stejnou plochu, mají pevné látky stejný objem.
Proto je objem mísy roven tomu, kde S = π R 2 je plocha základny kužele, plocha půlkule je ( komplementaritou ve válci) a plocha celé koule je .
Tyto metody, kde jsou roviny řezu stejné od jednoho tělesa k druhému, představují nejméně riskantní formu nedělitelné metody. Přesto však vyvolávají otázky: Galileo považuje za paradoxní, že poslední část kužele je bod a část mísy je kruh: zdá se mu, že bod a kruh nemohou mít stejný rozměr.
Paradox nedělitelných
Cavalieri si je dobře vědom, že jeho metoda zahrnuje rizika. Podle jeho principu, pokud jsou nedělitelné předměty v poměru k mezi dvěma čísly, jsou jejich plochy také v poměru k . Tento princip by nám nyní umožnil říci, že plocha trojúhelníku ABC a plocha trojúhelníku ADC by měla poměr k = 1 / L , zatímco víme, že tyto dvě oblasti jsou stejné.
Cavalieri si myslí, že tento paradox pramení ze skutečnosti, že jeho rozdělení nenásleduje stejnými směry, ale cítí se dobře s objevem dalších paradoxů, že jeho metoda zahrnuje riziko. Jeho žák Torricelli usiloval o řešení tím, že dal jednotlivcům tloušťku, čímž se otevřely dveře integrálnímu počtu: pro Torricelliho jsou jednotlivce trojúhelníku ABC silnější než trojúhelníky ADC.
Pascal se ve své Traite de la roulette (1659) s touto „tloušťkou“ vyrovná správně a dokonce uvede metodu integrace po částech. Všechny tyto výpočty však zůstávají v doméně kombinatoriky : je třeba vzít v úvahu ještě jeden krok k zohlednění nerovného rozdělení; pojem změny proměnné je přítomen v Isaacu Barrowovi současně (1660); ale právě u Gottfrieda Wilhelma Leibnize bude „ počet “ vzkvétat. Naopak ombral kámen z Gian-Carlo Rota se znovu objeví vazba mezi kombinatorika-diskrétní kalkulu a analýze.
Podívejte se také
Bibliografie
- (en) Kirsti Andersen , „ Cavalieriho metoda nedělitelných “ , Arch. Hist. Přesné Sci. , sv. 31, n O 4,1985, str. 261-367 ( číst online )
- Historie oblastí , Les Cahiers de l ' IREM d'Orléans, n o 3 [ on-line prezentace ] ".pdf" (verze 28. září 2007 o Internetového archivu ) , na archive.org