Quadric

V matematiky , s quadric nebo kvadratické plochy , je povrch uspokojující polynom kartézské rovnice ve stupni 2 se třemi proměnnými (obecně zaznamenána, x , y a z, ) ve formě:

Ax2+By2+Cz2+2Dyz+2Exz+2Fxy+Gx+Hy+Iz+J=0{\displaystyle Ax^{2}+By^{2}+Cz^{2}+2Dyz+2Exz+2Fxy+Gx+Hy+Iz+J=0}.

Tyto povrchy jsou klasifikovány redukovanou rovnicí v ortonormálním souřadnicovém systému přizpůsobeném v euklidovské geometrii a v devíti nedegenerovaných třídách až po lineární transformaci v afinní geometrii . Mohou být také studovány v rámci projektivní geometrie , která výsledky zcela zjednodušuje a sjednocuje.

Jejich rovinné části jsou kuželovité .

Definice je zobecnit do vyšší dimenze s myšlenkou afinní quadric , je hypersurface , charakterizované jako místo zrušení  (v) polynomu stupně 2, a to i na jiném těle koeficientů, než je z reálných čísel .

Klasifikace

Prezentace hlavních kvadrik

Nedegenerované kvadriky jsou popsány níže z jejich redukovaných rovnic ve vhodném ortonormálním rámci.

elipsoid	x2a2+y2b2+z2c2−1=0{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}-1=0\,} ,
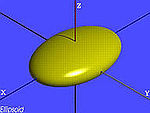
Jeden listů hyperboloid (H1)	x2a2+y2b2−z2c2−1=0{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}-1=0\,} ,
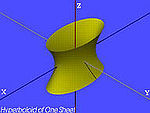
Hyperboloid se dvěma listy (H2)	x2a2+y2b2−z2c2+1=0{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}+1=0\,} ,
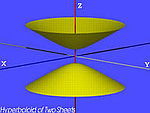
Eliptický paraboloid (PE)	x2a2+y2b2=z{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=z\,} ,
Hyperbolický paraboloid (PH)	x2a2−y2b2=z{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=z\,} ,
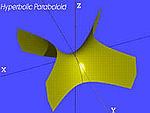
Eliptickou základnu kužele	x2a2+y2b2−z2c2=0{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0\,} ,
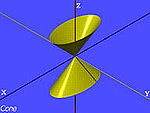
Eliptický válec	x2a2+y2b2−1=0{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-1=0\,} ,
Hyperbolické válec	x2a2−y2b2−1=0{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-1=0\,} ,
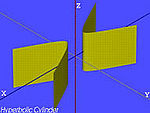
Parabolický válec	x2=2py{\displaystyle \displaystyle {x^{2}=2py}} .

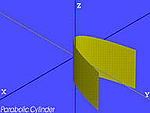
Obecná klasifikace

Rovnici povrchu lze napsat:

Q(x,y,z)+Gx+Hy+Iz+J=0 {\displaystyle Q(x,y,z)+Gx+Hy+Iz+J=0~}

kde Q označuje kvadratickou formu

Q(x,y,z)=Ax2+By2+Cz2+2Dyz+2Exz+2Fxy {\displaystyle Q(x,y,z)=Ax^{2}+By^{2}+Cz^{2}+2Dyz+2Exz+2Fxy~}

matice:

MQ=(AFEFBDEDC){\displaystyle M_{Q}={\begin{pmatrix}A&F&E\\F&B&D\\E&D&C\end{pmatrix}}}

jejichž vlastní čísla jsou reálná, protože tato matice je skutečná symetrická .

Podpis kvadratické formy je dvojice (p, q), kde p je počet pozitivních striktně čísel z Q a Q se počet přísně záporných čísel. Hodnost Q je pak p + q . Podle definice kvadrika nemůže být hodnost Q nulová. Skutečnost, že podpis kvadratické formy nezávisí na volbě zvoleného základu, dokazuje Sylvesterův zákon setrvačnosti .

Když je pozice rovna 3, quadric připouští střed symetrie.

Hodnost	Podpis	Nedegenerovaný kvadrik	Degenerovaný kvadrik
3	(3,0) nebo (0,3)	elipsoid	∅{\displaystyle \varnothing } nebo bod
	(2,1) nebo (1,2)	hyperboloid s 1 nebo 2 vrstvami nebo kuželem
2	(2,0) nebo (0,2)	eliptický paraboloid nebo eliptický válec	∅{\displaystyle \varnothing } nebo vpravo
	(1.1)	hyperbolický paraboloid nebo hyperbolický válec	setkání dvou plánů
1	(1,0) nebo (0,1)	parabolický válec	∅{\displaystyle \varnothing } nebo plán nebo kombinace dvou plánů

Demonstrace

Pro zjednodušení, souřadnice vždy třeba poznamenat, x , y a Z , po různých změnách ortonormální referenčních značek, které budou následovat.

Matice kvadratické formy, čisté jmenovité hodnoty , , je diagonalized použitím ortogonální transformační matice. V novém ortonormálním souřadnicovém systému je zapsána rovnice povrchu α {\displaystyle \alpha ~}β {\displaystyle \beta ~}γ {\displaystyle \gamma ~}

αx2+βy2+γz2+px+qy+rz=k {\displaystyle \alpha x^{2}+\beta y^{2}+\gamma z^{2}+px+qy+rz=k~}.

Když je například jedno z vlastních čísel nenulové, je možné vycentrovat odpovídající souřadnici: α {\displaystyle \alpha ~}

αx2+px=α((x+p2α)2−(p2α)2){\displaystyle \alpha x^{2}+px=\alpha ((x+{\frac {p}{2\alpha }})^{2}-({\frac {p}{2\alpha }})^{2})}

což se rovná provedení překladu nebo změně původu referenčního rámce.

• Když je pořadí rovno třem, tři vlastní čísla nejsou nula; v novém ortonormálním souřadnicovém systému se rovnice stává:

αx2+βy2+γz2=K {\displaystyle \alpha x^{2}+\beta y^{2}+\gamma z^{2}=K~}.

• • pokud má podpis hodnotu (3,0) nebo (0,3), mají tři vlastní čísla stejné znaménko. Pokud K je nula, je to bod; jinak je elipsoid, pokud má K znaménko vlastních čísel a prázdné sady jinak.
  • pokud má podpis hodnotu (2,1) nebo (1,2), dvě vlastní čísla mají stejné znaménko, které zde řekne většina; pokud K je nula, je to kužel; jinak je hyperboloid jednoho listu, pokud má K znaménko většiny, a jinak hyperboloid dvou listů .

• Když je pořadí rovno dvěma, jeden z vlastních čísel je nula a například jen jeden ; v novém ortonormálním souřadnicovém systému se rovnice stává:γ {\displaystyle \gamma ~}

αx2+βy2+rz=K {\displaystyle \alpha x^{2}+\beta y^{2}+rz=K~}.

• • pokud r je nenulová, získáme eliptický paraboloid, pokud mají dvě nenulová vlastní čísla stejné znaménko, a hyperbolický paraboloid jinak, protože rovnice je zapsána:

αx2+βy2=−r(z−Kr{\displaystyle \alpha x^{2}+\beta y^{2}=-r(z-{\frac {K}{r}}}).

• • jestliže r je nula, a pokud K je nula, jedná se o spojení dvou rovin, pokud nenulová vlastní čísla mají opačné znaménko a jinak přímku;
  • pokud r je nula a K nenulová, jedná se o hyperbolický válec, pokud nenulová vlastní čísla mají opačné znaménko, a pokud ne, eliptický válec, když K je znaménko nenulových vlastních čísel, a Jinak prázdná sada.

• Když je pozice rovna jedné, je například pouze jedna vlastní hodnota nenulová ; v novém ortonormálním souřadnicovém systému se rovnice stává:β {\displaystyle \beta ~}

βy2+px+qy=K  {\displaystyle \beta y^{2}+px+qy=K~~},

pak po poslední změně ortonormálního souřadného systému

βy2+Px=L  {\displaystyle \beta y^{2}+Px=L~~}.

Pokud P je nula, dostaneme rovinu, pokud L je nula, a spojení dvou rovin nebo prázdné množiny, v závislosti na tom, zda L je znaménko nebo ne. Jinak je to parabolický válec. β{\displaystyle \beta }

Klasifikace v afinní geometrii

Klasifikace v projektivní geometrii

Quadric v jakékoli dimenzi

Obecněji řečeno, v prostoru dimenze D, pokud jsou souřadnice prostoru , je obecná kvadricka hyperplocha definovaná algebraickou rovnicí: {x1,x2,…,xD}{\displaystyle \{x_{1},x_{2},\dots ,x_{D}\}}

∑i,j=1DQi,jxixj+∑i=1DPixi+R=0{\displaystyle \sum _{i,j=1}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=1}^{D}P_{i}x_{i}+R=0}

pro konkrétní výběr Q, P a R.

Normalizovaná rovnice pro nedegenerovaný kvadrik se středem v počátku má tvar:

∑i=1D±xi2ai2=1{\displaystyle \sum _{i=1}^{D}\pm {x_{i}^{2} \over a_{i}^{2}}=1}

Aplikace

V modelování obrazu

Pro povrch rovnice poskytuje Taylor-Youngův vzorec lokální aproximaci povrchu pomocí kvadrika rovnice: z=f(x,y) {\displaystyle z=f(x,y)~}

p(x−a)+q(y−b)+12[r(x−a)2+2s(x−a)(y−b)+t(y−b)2]{\displaystyle p(x-a)+q(y-b)+{\frac {1}{2}}[r(x-a)^{2}+2s(x-a)(y-b)+t(y-b)^{2}]}

s takzvanými Mongeovými notacemi p=∂f∂x(a,b),q=∂f∂y(a,b),r=∂2f∂x2(a,b),t=∂2f∂y2(a,b),s=∂2f∂x∂y(a,b).{\displaystyle p={\frac {\partial f}{\partial x}}(a,b),q={\frac {\partial f}{\partial y}}(a,b),r={\frac {\partial ^{2}f}{\partial x^{2}}}(a,b),t={\frac {\partial ^{2}f}{\partial y^{2}}}(a,b),s={\frac {\partial ^{2}f}{\partial x\partial y}}(a,b).}

Tato místní aproximace se používá při modelování obrazu, kde poskytuje zajímavé výsledky.

Poznámky a odkazy

1. André Warusfel , „Quadriques“ , Slovník matematiky, algebry, analýz, geometrie , Encyklopedie Universalis a Albin Michel,1997.
2. Ani prázdný, ani redukovaný na bod, úsečku, rovinu nebo spojení dvou rovin.
3. Sylvie Philipp, Strukturální modelování textury. Extrakce primárního zrna a pravidlo jeho umísťování ve dvanáctém colloque Gretsi , Juan-les-Pins, 1988, Číst online , str.  590 .
4. Alaa Mustafa, Příspěvek ke studiu diskrétních křivek a jejich aplikací , 2008 [Diplomová práce].

Podívejte se také

• Kuželovitý

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">