Indukční limit

V matematice , konkrétněji v teorii kategorií a univerzální algebře , pojem indukční meze zobecňuje struktury klasického pojmu meze vyplývajícího z analýzy .

Úvodní slovo

Induktivní limit je v teorii kategorií zvláštním případem kolimitu . Stejně jako jeho dvojí, projektivní limit , je koncepčně velmi blízký pojmu limitu, s nímž se při analýze setkáváme, a v určitých případech se s ním shoduje.

Prvním klíčovým bodem je pojem překročení limitu. Limit kladných reálných čísel je kladný. Limita druhé odmocniny se rovná druhé odmocnině limitu. Podobně , v algebře zjistíme, jaké jsou vlastnosti, které přecházejí k limitu (induktivní, projektivní nebo jiné). Těmito vlastnostmi nebudou funkce jako v analýze, ale funktory . Kovariantní funktor kompatibilní s indukčním limitem tedy zajistí, aby se indukční limit obrazů rovnal obrazu indukčního limitu. (Pokud je funktor kontravariantní, transformuje indukční limit na projektivní limit.)

Například v kategorii modulů na komutativním kruhu A stále existuje indukční limit, který je kompatibilní s jádrem , obrázkem a jádrem . Na druhou stranu je projektivní limit kompatibilní s jádrem, ale ne s obrazem.

Některé stavby jsou postaveny přirozeně překročením limitu. Pro nekonečné algebraické rozšíření lze skupinu Galois definovat projektivním limitem. Tímto způsobem získáváme ziskovou skupinu .

Druhým klíčovým bodem je pojem hustoty. Jakékoli reálné číslo je omezeno na racionální čísla a dokonce na desetinná místa (což je základem manipulace s čísly pomocí kalkulaček). Jakákoli spojitá funkce definovaná na segmentu je jednotným limitem polynomiálních funkcí a dokonce i funkcí stupňovitých. Tento výsledek umožňuje například oslnivou demonstraci Riemann-Lebesgueovy věty . Nejprve dokážeme výsledek pro funkce schodiště a pak jdeme na hranici. Právě tento stav mysli se snažíme reprodukovat v algebře díky indukčním limitům . Namísto přímého předvedení výsledku začneme jeho předváděním na jednoduchých objektech, poté přejdeme k indukční hranici. Můžeme si například všimnout, že jakýkoli vektorový prostor je indukční mezí konečných rozměrných vektorových prostorů.

Historická poznámka

Pojem indukčního limitu zavedl v roce 1931 Lev Pontriaguine, aby stanovil izomorfismus kvocientů podle své torzní podskupiny skupin homologie a (Betti skupiny s hodnotami v  ; pro skupinu Betti má hodnost odpovídající Bettiho číslo , konkrétně její hodnost ) kde X je libovolná kompaktní podmnožina . Skupiny , kde je klesající posloupnost kompaktních jednoduchých komplexů průsečíků rovna X , tvoří přímý systém abelianských skupin, kterými je „limitní skupina“ („Limesgruppe“) (tj. Induktivní limit). Pontriagin definoval docela obecně, a stejně jako my dnes, indukční limit přímého systému skupin (ne nutně Abelians). Očekávaným výsledkem je, že aplikace Hp(X;Z/mZ){\ displaystyle H_ {p} (X; \ mathbb {Z} / m \ mathbb {Z})}Hne-p-1(Rne-X;Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -X; \ mathbb {Z} / m \ mathbb {Z})}Z/mZ{\ displaystyle \ mathbb {Z} / m \ mathbb {Z}}m=0{\ displaystyle m = 0}Rne{\ displaystyle \ mathbb {R} ^ {n}}Hne-p-1(Rne-NE(Tj);Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z})}(NE(Tj)){\ displaystyle (N (T_ {j}))}Hne-p-1(Rne-X;Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -X; \ mathbb {Z} / m \ mathbb {Z})}

Hp(NE(Tj+1);Z/mZ)→Hp(NE(Tj);Z/mZ){\ displaystyle H_ {p} (N (T_ {j + 1}); \ mathbb {Z} / m \ mathbb {Z}) \ rightarrow H_ {p} (N (T_ {j}); \ mathbb {Z } / m \ mathbb {Z})}, Hne-p-1(Rne-NE(Tj);Z/mZ)→Hne-p-1(Rne-NE(Tj+1);Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z}) \ rightarrow H_ {np-1} ( R ^ {n} -N (T_ {j + 1}); \ mathbb {Z} / m \ mathbb {Z})}

jsou vzájemně transponovány. Sled forem tvoří inverzní systém, jehož (projektivní) mez je  ; Pontriagin nicméně postrádal pojem projektivní hranice, který viděl Eduard Čech v následujícím roce (1932) nezávisle na Pontriaginově díle; ale přesnou definici projektivní meze inverzního systému topologických prostorů podal až v roce 1936 Norman Steenrod . Formulace projektivních (resp. Indukčních) limitů skupin nebo topologických skupin nebo topologických prostorů atd. jako funktory mezi kategorií přímých (resp. inverzních) systémů a konkrétní kategorií skupin nebo topologických skupin nebo topologických prostorů atd. provedli v roce 1945 Samuel Eilenberg a Saunders Mac Lane  ; tyto pojmy a jejich vztahy byly formulovány zcela obecně a podrobně studovány Danielem Kanem (en) v roce 1958. Hp(NE(Tj);Z/mZ){\ displaystyle H_ {p} (N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z})}Hp(X;Z/mZ){\ displaystyle H_ {p} (X; \ mathbb {Z} / m \ mathbb {Z})} 

Objednaná filtrační sada

Dovolit být uspořádaná množina (částečně objednaná obecně). Říkáme, že se jedná o filtrovanou uspořádanou množinu if (Já,≤){\ displaystyle (I, \ leq)}(Já,≤){\ displaystyle (I, \ leq)}

∀(i,j)∈Já2,∃k∈Já,i≤k Et j≤k.{\ displaystyle \ forall (i, j) \ v I ^ {2}, \ existuje k \ v I, i \ leq k \ a \ j \ leq k.}

Říkáme, že sada filtruje nalevo, když filtruje opačné pořadí . V takovém případě slovní zásobu ponecháme, ale bude odpovídat opačnému pořadí. V praxi to nezpůsobuje zmatek, je to dokonce spíše praktické. Filtrační sada I je kategorie, jejíž objekty jsou prvky I a morfismy jsou dvojice (zdroje i a cíle j ). (j,i),i≤j{\ displaystyle (j, i), i \ leq j}

Indukční systém

Nechť je objednaná filtrační sada. Pojďme být kategorií. Nazýváme indukční systém objektů indexovány I se funktor (kovariantní) ve I v údaje o rodině předmětů a morfismů pro každou dvojici indexů tak, že se celá splňující: (Já,≤){\ displaystyle (I, \ leq)}VS{\ displaystyle {\ mathcal {C}}}D{\ displaystyle {\ mathfrak {D}}}VS{\ displaystyle {\ mathcal {C}}}VS{\ displaystyle {\ mathcal {C}}}(Ei)i∈Já{\ displaystyle (E_ {i}) _ {i \ v I}}VS{\ displaystyle {\ mathcal {C}}}Fij:Ei→Ej{\ displaystyle f_ {i} ^ {j}: E_ {i} \ až E_ {j}}(i,j)∈Já2{\ displaystyle (i, j) \ v I ^ {2}}i≤j{\ Displaystyle i \ leq j}

• ∀i∈Já,Fii=JádEi{\ displaystyle \ forall i \ in I, f_ {i} ^ {i} = Id_ {E_ {i}}} ;
• ∀(i,j,k)∈Já3, i≤j≤k⇒Fjk∘Fij=Fik{\ displaystyle \ forall (i, j, k) \ v I ^ {3}, \ i \ leq j \ leq k \ Rightarrow f_ {j} ^ {k} \ circ f_ {i} ^ {j} = f_ {i} ^ {k}}.

Tento funktor je definován a . D(i)=Ei{\ displaystyle {\ mathfrak {D}} (i) = E_ {i}}D((i,j))=Fij{\ displaystyle {\ mathfrak {D}} ((i, j)) = f_ {i} ^ {j}}

Univerzální vlastnost indukčního limitu

Nechť ( X i , f ij ) je indukční systém v kategorii . Indukční mez X , pokud existuje, je předmětem kategorie opatřené šipkami z X i s hodnotami v X , které ověřují vztahy kompatibilitu pro všechny . Kromě toho musí být data univerzální: pro jakýkoli jiný objekt Y vybavený rodinou šipek family i ověřující podobnou kompatibilitu existuje jediná šipka u  : X → Y , například diagram: VS{\ displaystyle {\ mathcal {C}}} VS{\ displaystyle {\ mathcal {C}}}ϕi{\ displaystyle \ phi _ {i}}ϕi=ϕj∘Fij{\ displaystyle \ phi _ {i} = \ phi _ {j} \ circ f_ {ij}}i≤j{\ Displaystyle i \ leq j}(X,ϕi){\ displaystyle (X, \ phi _ {i})}

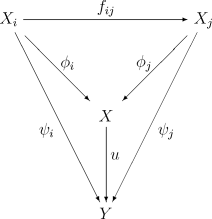
buďme komutativní pro všechna i ≤ j . Indukční limit je uvedeno: . Budeme hovořit o indukční hranici X i podle přechodových morfismů f ij , nebo zneužitím jazyka, o limitě podle I , viz zcela jednoduše o indukční hranici X i . X=lim→⁡Xi{\ displaystyle X = \ varinjlim X_ {i}}

Stejně jako u jakékoli univerzální vlastnosti , pokud existuje, je indukční limit jedinečný, až do jednoho izomorfismu.

Jinými slovy, indukční limit představuje funktor, který sdružuje množinu s objektem Y kategorie . VS{\ displaystyle {\ mathcal {C}}}lim←⁡HÓm(Xi,Y){\ displaystyle \ varprojlim Hom (X_ {i}, Y)}

Konstrukce indukčního limitu

Indukční limit existuje ve většině obvyklých kategorií (zejména magma , monoidy , skupiny , Abelovy skupiny , prsteny , A- moduly , K- vektorové prostory , topologické prostory atd.). Můžeme to postavit z indukčního limitu rodiny základních sad. Dojíždí proto s funktorem zapomínání.

Obecněji řečeno, v jakékoli kategorii je jeho konstrukce dvojí oproti konstrukci projektivního limitu . Konstruktivní limit konstruujeme pomocí dvou procesů, produktu a jádra . Konstruujeme induktivní limit ze dvou duálních pojmů součet a cokernel .

Indukční nastavený limit

Nechť ( E i , f ij ) je indukční soustava množin. Získáme induktivní limitu jako kvocientu na disjunktní sjednocení strany vztahu ekvivalence  : ⊔i∈JáEi{\ displaystyle \ sqcup _ {i \ in I} E_ {i}}

(i,X)∼(j,y)⇔∃k∈Já,i≤k, j≤k Et Fik(X)=Fjk(y){\ displaystyle (i, x) \ sim (j, y) \ Leftrightarrow \ existuje k \ v I, i \ leq k, \ j \ leq k \ a \ f_ {i} ^ {k} (x) = f_ {j} ^ {k} (y)}

Označme množinu kvocientů. Definujeme , vezmeme to jako třídu . E∞{\ displaystyle E _ {\ infty}}ϕi:Ei→E∞{\ displaystyle \ phi _ {i}: E_ {i} \ až E _ {\ infty}}ϕi(X){\ displaystyle \ phi _ {i} (x)}(i,X){\ displaystyle (i, x)}

Nechť ( E i , f ij ) je indukční systém topologických prostorů . V předchozí konstrukci jsme postupně obdarovali disjunktní sjednocení podkladových množin finální topologií , potom množinu kvocientů topologií kvocientu (nebo přímo: limitu indukční množiny jsme dali finální topologii).

Indukční mez magmat

Nechť ( E i , f ij ) je indukční systém magmat. Každá sada je opatřena zákonem o vnitřní kompozici a každá mapa je morfismem. Začneme konstrukcí indukčního limitu množin . Pak existuje jedinečná struktura magmatu na tom, že kanonické mapy jsou morfismy. Ei{\ displaystyle E_ {i}}∗i{\ displaystyle * _ {i}}Fij{\ displaystyle f_ {i} ^ {j}}Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}ϕi{\ displaystyle \ phi _ {i}}

Tento zákon konstruujeme následovně. Nechť a dva zástupci dvou prvků . Existují takové a . V , máme a . Poté jsme nastavili , získaný výsledek samozřejmě nezávisí na výběru . (i,X){\ displaystyle (i, x)}(j,y){\ displaystyle (j, y)}E∞{\ displaystyle E _ {\ infty}}k∈Já{\ displaystyle k \ v I}i≤k{\ Displaystyle i \ leq k}j≤k{\ displaystyle j \ leq k}E∞{\ displaystyle E _ {\ infty}}(i,X)=(k,Fik(X)){\ displaystyle (i, x) = (k, f_ {i} ^ {k} (x))}(j,y)=(k,Fjk(y)){\ displaystyle (j, y) = (k, f_ {j} ^ {k} (y))}(i,X)∗(j,y)=(k,Fik(X)∗kFjk(y)){\ displaystyle (i, x) * (j, y) = (k, f_ {i} ^ {k} (x) * _ {k} f_ {j} ^ {k} (y))}k{\ displaystyle k}

Vlastnosti

• Jestliže každý zákon je komutativní , pak zákon * je komutativní.∗i{\ displaystyle * _ {i}}
• Jestliže každý zákon je asociativní , pak zákon * asociativní.∗i{\ displaystyle * _ {i}}
• Pokud má každý zákon neutrální prvek a pokud každý morfismus vyhovuje , pak * má neutrální e (navíc pro každé i máme ).∗i{\ displaystyle * _ {i}} Ei{\ displaystyle e_ {i}}Fij{\ displaystyle f_ {i} ^ {j}}Fij(Ei)=Ej{\ displaystyle f_ {i} ^ {j} (e_ {i}) = e_ {j}}ϕi(Ei)=E{\ displaystyle \ phi _ {i} (e_ {i}) = e}
• Pokud má každý strukturu skupiny , jedná se o skupinu.Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}

Limit indukčního vyzvánění

Podobně, pokud má každá sada dva zákony a , má indukční limit dva zákony a . Pokud je každý zákon distribuční s ohledem na , pak je distribuční s ohledem na . Ei{\ displaystyle E_ {i}}+i{\ displaystyle + _ {i}}∗i{\ displaystyle * _ {i}}E∞{\ displaystyle E _ {\ infty}}+{\ displaystyle +}∗{\ displaystyle *}∗i{\ displaystyle * _ {i}}+i{\ displaystyle + _ {i}}∗{\ displaystyle *}+{\ displaystyle +}

Tento proces tak umožňuje konstrukci limitu indukčního kruhu.

• Pokud je každý prsten neporušený, je tomu tak .Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}
• Pokud je každý prsten tělo, tak je také .Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}

Induktivní limit modulů

Nechť A je komutativní kruh a ( E i , f ij ) indukční systém A- modulů . Můžeme vybavit indukční limit podkladových množin strukturou A- modulu tak, aby mapy byly lineární. Taková struktura je jedinečná a je konstruována stejným způsobem jako u magmat. E∞{\ displaystyle E _ {\ infty}}ϕi{\ displaystyle \ phi _ {i}}

Příklady

• V případě, že filtrační sestava I má větší element (například v případě, I je konečný a není prázdná), indukční omezení jakéhokoliv indukčního systému je rovna .ω{\ displaystyle \ omega}(Ei,Fij){\ displaystyle (E_ {i}, f_ {i} ^ {j})}Eω{\ displaystyle E _ {\ omega}}
• Počáteční objekt je indukční limit systému indexovaného prázdnou sadou .
• Nechť E je množina a rostoucí posloupnost podmnožin E , s kanonickými injekcemi. Indukční limit sekvence je identifikován spojením těchto sad.(Ene){\ displaystyle (E_ {n})}(Ene){\ displaystyle (E_ {n})}
• Nechť p je prvočíslo . U všech n ať U n je cyklická skupina p n -tých kořenů jednoty v algebraicky uzavřeném poli. Považujeme inkluze za přechodové morfismy. Přímá hranice tohoto systému je pak nekonečný skupina složená ze všech p- primárních kořenů jednoty (viz skupinu Prufer v ).
• Nechť E být topologický prostor a v bodu E, zárodek funkcí E v je induktivní limit souborů ze sad spojitých zobrazení libovolného sousedství U všech . Sousedství seřazená podle zahrnutí (filtrování doleva, které obrací směr šipek). Protože jdeme dovnitř omezením.R{\ displaystyle \ mathbb {R}}VS(U,R){\ displaystyle C (U, \ mathbb {R})}PROTI⊂U{\ displaystyle V \ podmnožina U}VS(U,R){\ displaystyle C (U, \ mathbb {R})}VS(PROTI,R){\ displaystyle C (V, \ mathbb {R})}

Poznámky a odkazy

1. (De) Lev Pontriaguine , „  Über den algebraischen Inhalt topologische Dualitätssätze  “ , Mathematische Annalen , sv.  105,1931, str.  165-205 ( číst online ).
2. Eduard Čech , „  Obecná teorie homologie v jakémkoli prostoru  “, Fundamenta Mathematicae , sv.  19,1932, str.  149-183 ( číst online [PDF] ).
3. (in) Norman Steenrod , „  Universal homology groups  “ , American Journal of Mathematics , sv.  58, n O  4,1936, str.  661-701 ( číst online ), str. 664.
4. (in) Jean Dieudonne , Historie algebraické a diferenciální topologie 1900-1960 , Birkhauser,1989( číst online ).
5. (in) Samuel Eilenberg a Saunders MacLane , „  General Theory of Equivalence  “ , Transaction of the American Mathematical Society , sv.  58, n O  2 1945, str.  231-294 ( číst online [PDF] ).
6. (in) Daniel Kan , „  náměstci funktorů  “ , Transaction of the American Mathematical Society , sv.  87, 1958, str.  294-329 ( číst online [PDF] ).

Zdroje

• Teorie Régine a Adrien Douady , Algebra a Galois [ detail vydání ]
• N. Bourbaki , Algebra , kapitoly 1 až 3

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">