Vzepětí skupina

V matematiky se vzepětí skupina o řád 2 n , o nenulové přirozené číslo n , je skupina , která je interpretována zejména skupiny isometries roviny vedení pravidelný mnohoúhelník s n stranami. Skupinu tvoří n prvků odpovídajících rotacím a n dalších odpovídajících odrazům . To je označeno D n některými autory a D 2 n jinými. Použijeme zde notaci D2 n .

Skupina D 2 je cyklická skupina řádu 2, označené C 2 ; skupina D 4 je skupina Klein se čtyřmi prvky. Mezi diedrickými skupinami D 2 n jsou jediní dva, kteří jsou abelianští . Interpretace dihedrálních skupin jako skupin izometrií není pro tyto dva speciální případy vhodná, protože neexistují žádné pravidelné polygony s jednou nebo dvěma stranami. Někteří autoři definují pouze dihedrickou skupinu řádu 2 n pro n alespoň rovnou 3. Avšak skupinu D 4 lze interpretovat jako skupinu izometrií roviny udržující segment nezredukovaný na bod.

Prezentace a ekvivalentní definice

Skupina D 2 n může být definována následujícím přesným rozdělením sekvence :

{\ displaystyle 1 \ až C_ {n} \ až D_ {2n} \ až C_ {2} \ až 1}

kde C n (také uvedeno Z n nebo Z / n Z ) je cyklická skupina řádu n , C 2 je cyklická řádu 2, část je dána působením čtení $σ$ generátoru C 2 , na a generátor $τ$ cyklické skupiny řádu n :

\ sigma \ tau \ sigma ^ {{- 1}} = \ tau ^ {{{- 1}}.

Tato skupina je tedy částečně přímým produktem z C n o C 2 po Morfizmus $ln$ , kde jednotka C 2 působí na C n jako identické mapy a druhý prvek C 2 zákonů o C n inverzí. Výslovně:

{\ text {si}} \; C_ {n} = \ langle \ tau \ rangle, \; C_ {2} = \ langle \ sigma \ rangle \; {\ text {then}} \; \ psi (1) (\ tau ^ {k}) = \ tau ^ {k}, \ psi (\ sigma) (\ tau ^ {k}) = \ tau ^ {{- k}} \ quad \ forall k \ in \ {0 , 1,2, ..., n-1 \}.

Prezentace je pak:

{\ displaystyle \ left \ langle \ sigma, \ tau \ mid \ sigma ^ {2}, \ tau ^ {n}, \ sigma \ tau \ sigma ^ {- 1} \ tau \ pravý \ rangle,}

tj. generátory jsou $σ$ , $τ$ a jediné vztahy, které uspokojí, jsou ty, které vyplývají (podle axiomů o zákoně skupiny) z:

{\ displaystyle \ sigma ^ {2} = 1, \ quad \ tau ^ {n} = 1 \ quad {\ text {a}} \ quad \ sigma \ tau \ sigma ^ {- 1} = \ tau ^ {- 1}.}

Můžeme tedy sestavit kompletní seznam prvků skupiny:

1, \ tau, \ tau ^ {2}, \ dots, \ tau ^ {{n-1}}, \ sigma, \ sigma \ tau, \ sigma \ tau ^ {2}, \ dots, \ sigma \ tau ^ {{n-1}}

Alternativní prezentace, kde $μ = τσ$ v generátorovém systému předchozí prezentace, je:

{\ displaystyle \ left \ langle \ sigma, \ mu \ mid \ sigma ^ {2}, \ mu ^ {2}, (\ mu \ sigma) ^ {n} \ pravý \ rangle,}

to znamená, že generátory jsou $σ$ , $μ$ a jediné vztahy, které uspokojí, vyplývají z:

{\ displaystyle \ sigma ^ {2} = 1, \ quad \ mu ^ {2} = 1 \ quad {\ text {a}} \ quad (\ mu \ sigma) ^ {n} = 1.}

Vidíme tedy, že dihedrální skupina připouští soustavu dvou odlišných generátorů obou řádu 2. Dihedrální skupiny jsou jediné konečné skupiny, které mají tuto vlastnost.

Dihedrální skupině řádu 2, n může také být viděn jako skupina automorphisms v grafu se skládá pouze z cyklu s n vrcholy (je-li n ≥ 3).

Geometrická interpretace

Můžeme definovat reprezentaci vzepětí skupiny D 2n následovně :

{\ displaystyle \ varphi: D_ {2n} \ do \ mathrm {GL} _ {2} (\ mathbb {R})}

{\ text {with}} \ quad \ varphi (\ tau) = {\ begin {pmatrix} \ cos (2 \ pi / n) & - \ sin (2 \ pi / n) \\\ sin (2 \ pi / n) & \ cos (2 \ pi / n) \ end {pmatrix}} \ quad {\ text {et}} \ quad \ varphi (\ sigma) = {\ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix}}.

Toto znázornění je ve skutečnosti s hodnotami v ortogonální skupině O (2, R ).

Uznáváme, že matice $φ (τ)$ je rotační matice úhlu $2π / n$ a matice $φ (σ)$ reflexní matice. Tyto transformace účinně ponechávají pravidelný mnohoúhelník se středem v počátku s n stranami neměnnými .

Cyklický graf

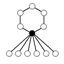
Tyto grafy cyklů z dihedral skupin se skládá z n- prvek cyklu a 2-prvků cyklů. Tmavý vrchol v cyklických grafech různých dihedrálních skupin představuje prvek identity a ostatní vrcholy jsou dalšími prvky skupiny. Cyklus se skládá z postupných sil jednoho nebo druhého prvku připojeného k prvku identity .


D 4	D 6	D 8	D 10	D 12	D 14

Vlastnosti

Podskupina $⟨τ⟩$ = { $1, τ, τ 2 ,\dots, τ n -1$ } rotací je normální a sudá, je-li n ≥ 3, charakteristická .

Některé vlastnosti diedrických skupin D 2 n s n ≥ 3 závisí na paritě n . Často je lze snadno odvodit z geometrického vyjádření této skupiny.

Centrum Z ( D 2 n ) z D 2 n se skládá pouze z totožnosti, pokud n je zvláštní, ale pokud n je dokonce centrum má dva prvky: identitu a prvek $▼ je$ n / 2 , tak, aby se podíl skupina D 2 n / Z ( D 2 n ) je izomorfní s D 2 n, pokud n je liché, a D n, pokud n je sudé. Proto je dihedrální skupina nilpotentní právě tehdy, je-li její řád mocninou dvou, a nilpotenční třída dihedrální skupiny řádu 2 r , s r > 1, se rovná r - 1.
Sub- skupina derivát z D 2 n je $⟨[σ, τ] =⟩ ⟨τ 2 ⟩$ (rovná $⟨τ⟩$ , pokud n je liché). Skupina D 2 n je tedy řešitelná pro třídu ≤ 2 (třídy 2, pokud n ≥ 3, a třídy 1, pokud n = 1 nebo 2). Dihedrální skupiny tak ilustrují skutečnost, že třídu nilpotence nilpotentní skupiny nelze zvýšit podle její třídy resolubility (zatímco její třída resolubility může být zvýšena podle její třídy nilpotence ).
Pro liché n , skupina D 4 n je izomorfní na přímý produkt z D 2 n a cyklické skupině řádu 2. Tento izomorfismus je dána vztahem: ${\ displaystyle D_ {4n} \ až D_ {2n} \ krát C_ {2}, \ quad \ sigma ^ {h} \ tau ^ {k + \ epsilon n} \ mapsto (\ sigma ^ {h} \ tau ^ {k}, \ epsilon)}$ h a je definováno modulo 2 a k modulo n . Generátory dihedrálních skupin jsou vybrány jako v první části článku. $\ epsilon$
V D 2 n jsou všechny odrazy navzájem konjugovány v případě, že n je liché, ale jsou obsaženy ve dvou třídách konjugace, pokud je n sudé.
Pokud m dělí n , pak D 2 n má n / m podskupiny typu D 2 m a cyklickou podskupinu C m . Proto je celkový počet podskupin D 2 n ( n ≥ 1) roven d ( n ) + σ ( n ), kde d ( n ) je počet kladných dělitelů n a σ ( n ) je součet kladných dělitelů n (viz seznam malých skupin pro případy n ≤ 8).

Zastoupení

Pokud je n liché, skupina D 2 n připouští 2 komplexní neredukovatelné reprezentace stupně 1:

\ sigma \ mapsto (-1) ^ {k} \; \ tau \ mapsto 1 \; k \ v \ {0,1 \}.

Na druhou stranu, pokud je n sudé, existují 4 neredukovatelné reprezentace stupně 1:

\ sigma \ mapsto (-1) ^ {k} \; \ tau \ mapsto (-1) ^ {h} \; k \ v \ {0,1 \} \; h \ v \ {0,1 \}.

Ostatní neredukovatelné reprezentace jsou stupně 2; jsou v počtu, pokud je $n$ liché, respektive pokud je $n$ sudé. Lze je definovat takto: ${\ frac {n-1} 2}$ ${\ frac n2} -1$

\ tau \ mapsto {\ begin {pmatrix} \ omega ^ {h} & ​​0 \\ 0 & \ omega ^ {{- h}} \ end {pmatrix}} \ quad {\ mbox {and}} \ quad \ sigma \ mapsto {\ begin {pmatrix} 0 & -1 \\ - 1 & 0 \ end {pmatrix}}

kde $ω$ označuje n- tý primitivní kořen jednoty a h prochází celá čísla mezi 1 a n - 1. Můžeme ověřit, že dvě takové reprezentace jsou izomorfní pouze pro h 1 a h 2 splňující h 1 + h 2 = n . Poté získáme oznámený počet neizomorfních neredukovatelných reprezentací stupně 2, a tedy všech neredukovatelných reprezentací dihedrální skupiny, vzorcem spojujícím počet neredukovatelných reprezentací s řádem skupiny .

Automorfismy

Skupina automorphisms z D 2 = Z 2 je triviální . Skupina Klein D 4 = Z 2 × Z 2 je neabelovská skupina řádu 6 : GL (2, F 2 ) ≃ S 3 ≃ D 6 (en) .

Pro n ≥ 3, skupina Aut ( D 2 n ) automorphisms D 2, n = Z n ⋊ Z 2 je holomorph Hol ( Z n ) = Z n ⋊Aut ( Z n ) ≃ Z n ⋊ Z× nz charakteristického podskupina Z n . Opravme prvek $σ$ z D 2 n \ Z n, potom pro jakýkoli automorfismus f z D 2 n označme h f prvek $σ$ f ( $σ$ ) a k f omezení f na Z n . Poté ověříme, že mapa f ↦ ( h f , k f ) je izomorfismem z Aut ( D 2 n ) do Z n ⋊Aut ( Z n ).

Pro n ≠ 2 je tedy skupina Aut ( D 2 n ) řádu n $φ$ ( n ), kde $φ$ je Eulerova indikatrix .

Podskupina interiérových automorphisms je izomorfní k D 2 n / z ( D 2 N ), tedy ( viz výše ), aby D 2, n , pokud n je liché, a D, n , pokud n je sudé.

Jediné hodnoty n, pro které mají dvě skupiny Aut ( D 2 n ) a D 2 n stejné pořadí, tj. Pro které $φ$ ( n ) = 2, jsou n = 3, 4 a 6. Pro tyto tři hodnoty, aut ( D 2 n ) ≃ Z n ⋊ Z×
n≃ Z n ⋊ Z 2 = D 2 n .

Nekonečná dihedrální skupina

Nekonečný vzepětí skupina (v) D ∞ je definován jako generalizované dihedrální skupiny ( viz níže ), z na nekonečné cyklické skupiny C ∞ = Z :

{\ displaystyle D _ {\ infty}: = Dih (\ mathbb {Z}) = \ mathbb {Z} \ rtimes C_ {2} = \ mathrm {Hol} (\ mathbb {Z}) = \ left \ langle \ sigma, \ tau \ mid \ sigma ^ {2}, \ sigma \ tau \ sigma ^ {- 1} \ tau \ right \ rangle.}

Nastavením $μ = τσ$ vidíme, že je izomorfní s volným produktem C 2 * C 2 :

{\ displaystyle D _ {\ infty} = \ left \ langle \ sigma, \ mu \ mid \ sigma ^ {2}, \ mu ^ {2} \ right \ rangle.}

Jeho střed je triviální.

Můžeme interpretovat D ∞ jako skupinu automorfismů grafu tvořenou nekonečnou cestou v obou směrech. Ekvivalentně je to skupina shodností v Z .

Aut ( D ∞ ) se rovná D ∞ ⋊ Z 2 , kde normální podskupina D ∞ sestává z vnitřních automorfismů a kde působení Z 2 na D ∞ = C 2 * C 2 spočívá ve výměně dvou faktorů. Proto:

{\ displaystyle Aut (D _ {\ infty}) = \ left \ langle \ sigma, \ mu, \ nu \ mid \ sigma ^ {2}, \ mu ^ {2}, \ nu ^ {2}, \ nu \ sigma \ nu \ mu ^ {- 1} \ right \ rangle = \ left \ langle \ sigma, \ nu \ mid \ sigma ^ {2}, \ nu ^ {2} \ right \ rangle \ simeq D _ {\ infty}.}

Zobecněná dihedrální skupina

Pro každý abelian skupiny H , zobecněný vzepětí skupina H , označený dihydroxy ( H ), je částečně přímým produktem z H o C 2 , působení C 2 na H je inverze, tj

{\ mathrm {Dih}} (H) = H \ rtimes _ {\ varphi} C_ {2},

kde φ (0) je mapa identity a φ (1) inverze prvku.

Takto získáme, pokud jsou H i C 2 oba aditivně zaznamenány:

( h 1 , 0) * ( h 2 , t 2 ) = ( h 1 + h 2 , t 2 ) ( h 1 , 1) * ( h 2 , t 2 ) = ( h 1 - h 2 , 1 + t 2 )

pro všechny h 1 , h 2 v H a t 2 v C 2 .

(Pokud je C 2 označeno násobením, lze tyto dva vzorce sečíst v ( h 1 , t 1 ) * ( h 2 , t 2 ) = ( h 1 + t 1 h 2 , t 1 t 2 ).)

Podskupina Dih ( H ), která obsahuje ve formě prvků ( h , 0), je normální podskupina z indexu 2 isomorfní H . Pokud jde o prvky formuláře ( h , 1), každý má svou vlastní inverzi.

Tyto třídy konjugace jsou

množiny {( h , 0), (- h , 0)};
množiny {( h + k + k , 1) | k v H }.

Pro jakoukoli podskupinu M z H tedy odpovídající prvky ( m , 0) také tvoří normální podskupinu Dih ( H ) izomorfní s M a máme:

Dih ( H ) / M = Dih ( H / M ).

Příklady:

D 2 n = Dih ( C n ).
- Pokud je n sudé, existují dvě množiny tvaru {( h + k + k , 1) | k v H } a každý z nich generuje normální podskupinu izomorfní s D n . Jedná se o dvě podskupiny skupiny izometrií pravidelného n -gone, izomorfní, ale odlišné: obě obsahují stejné rotace, ale v jedné ze dvou podskupin každý odraz fixuje dva vrcholy, zatímco v druhé odrazy ne opravit jakýkoli summit.
- Pokud je n liché, existuje pouze jedna množina tvaru {( h + k + k , 1) | k v H }.
D ∞ = dihydroxy ( Z ); existují dvě sady tvaru {( h + k + k , 1) | k v H } a každý z nich generuje podskupinu isomorfní k D ∞ . Jedná se o dvě podskupiny ze skupiny izometrií Z , izomorfní, ale odlišné: obě obsahují stejné překlady (sudými celými čísly), ale v jedné ze dvou podskupin má každá reflexe celočíselný pevný bod (její střed), zatímco v jiné jsou odrazy bez celočíselného pevného bodu (jejich středy jsou celá celá čísla ).
Dih (S 1 ) je izomorfní s ortogonální skupinou O (2, R ) izometrií euklidovské roviny, které fixují počátek nebo ekvivalentně ke skupině izometrií kruhu . Rotace tvoří skupina SO (2, R ), isomorfní aditivní skupiny R / Z , a také izomorfní na multiplikativní skupiny S 1 rovna kruhu jednotky (tvořené z komplexních čísel z modulu 1). V druhém případě je jednou z odrazů (která spolu s rotacemi generuje celou skupinu) složitá konjugace . Správné normální podskupiny obsahují pouze rotace. Diskrétní normální podskupiny jsou pro každé celé číslo n cyklickou podskupinou řádu n a kvocienty jsou izomorfní se stejnou skupinou Dih (S 1 ).
Dih ( R n ) je skupina centrálních překladů a symetrií R n (které, pokud n > 1 nevyčerpají všechny izometrie).
Dihydroxy ( H ) pro jakékoli podskupině R n , například diskrétní skupina ; v tomto případě, jedná-li v n směrech, jedná se o síť .
- Diskrétní podskupiny Dih ( R 2 ), které obsahují překlady pouze v jednom směru, jsou vlysové skupiny typů ∞∞ a 22∞.
- Ty, které obsahují překlady ve dvou směrech, jsou skupiny tapet typů p1 a p2.
- Podskupiny diskrétní Dih ( R 3 ), které obsahují překlady ve třech směrech, jsou prostorové grupy na retikulární triklinický systémů .

Dih ( H ) je abelian právě tehdy, když je polopřímý produkt přímý, tj. Právě tehdy, když každý prvek H je jeho vlastní inverzní, tj. H je elementární abelianská 2 skupina (en) : Dih ( C 2 k ) = C 2 k +1 .

Poznámky a odkazy

(fr) Tento článek je částečně nebo zcela převzat z článku Wikipedie v angličtině s názvem „ Dihedral group “ ( viz seznam autorů ) .

Zdá se, že tato notace začala převládat. (en) Joseph J. Rotman (en) , An Introduction to the Theory of Groups [ detail editions ], 1999, s. 68 ( vidět na Google Books ), údajně opustil D n ve prospěch D 2 n . J. Delcourt, Theorie des skupiny , 2 nd ed., Dunod, vydání z roku 2012, str. 27, používá notaci D 2 n .
To je případ (en) DJS Robinsona (de) , Kurz v teorii skupin , Springer,1996, 2 nd ed. ( číst online ) , s. 6.
Pohled (in) Mr. Aschbacher , Finite Group Theory , Cambridge University Press , 2000, str. 141, náhled v Knihách Google .
Rotman 1999 , teorie. 3,32, s. 68.
Rotman 1999 , cvičení 5,41, s. 118.
(in) C. Charles Richard Leedham-Green (in) a Susan R. McKay, The Structure of Groups of Prime Power Order , Oxford University Press, 2002 Horn. 3.3.4, (iii), str. 60–61, náhled v Knihách Google .
Viz například Polopřímý produkt # Odvozená skupina nebo tento problém opraven na Wikiversity .
Robinson 1996 , cvičení. 5.1.9, s. 128.
(en) F. Rotmaler, „ Automorfické skupiny dihedrálních skupin “ , Ukrainian Mathematical Journal , sv. 29, n O 21977, str. 162-167 ( DOI 10.1007 / BF01089242 ).
Robinson 1996 , str. 51.

Podívejte se také

Bibliografie

Jean-Pierre Serre , Lineární reprezentace konečných skupin [ detail vydání ]
Bernard Charles a Denis Allouch, General Algebra , Paříž, PUF, 1984

Související články