Geometrická algebra (struktura)

Geometrická algebra je v matematice , jako algebraické struktury , podobně jako na skutečném Clifford algebry , ale s geometrickým výkladem vyvinutý Davidem Hestenes , nástupu do práce Hermann Grassmann a William Kingdon Clifford (termín je také používán v obecnější smysl popsat studium a použití těchto algeber: geometrická algebra je studium geometrických algeber ). Nepochybný cíl tohoto teoretického fyzika a pedagoga je najít jazyk vhodný pro sjednocení symbolických manipulací ve fyzice, jehož mnoho oborů dnes praktikuje z historických důvodů různé formalizmy (tenzory, matice , torzory, vektorová analýza, použití komplexních čísel , spinory , čtveřice , diferenciální formy …) . Jméno zvolené Davidem Hestenesem ( geometrická algebra ) je jméno, které chtěl Clifford dát své algebře.

Geometrická algebra je užitečná ve fyzických problémech, které zahrnují rotace , fáze nebo imaginární čísla . Jeho navrhovatelé tvrdí, že poskytuje kompaktnější a intuitivnější popis kvantové a klasické mechaniky , elektromagnetické teorie a relativity . Současné aplikace geometrické algebry zahrnují počítačové vidění , biomechaniku, stejně jako robotiku a dynamiku vesmírných letů .

Dějiny

Od dávných vazeb mezi algebry a geometrie byli známí Řekům, ale základy systému, o nichž hovoříme byly založeny v XIX th století.

V roce 1843 William Rowan Hamilton objevil čtveřice, které interpretoval geometricky jako vektory (špatně). O rok později představil Hermann Günther Grassmann produkt pro interiér a exteriér, který umožňuje konstrukci algeber působících na geometrické objekty. A konečně, v roce 1873 se Williamovi Kingdonovi Cliffordovi podařilo integrovat výsledky Hamiltona a Grassmanna do první formulace geometrické algebry.

Cliffordův objev zůstává bez povšimnutí, pravděpodobně kvůli předčasné smrti jeho autora, a fyzikové z konce XIX th století nevěda tento matematický nástroj začít používat jiný systém známý jako „vektorového počtu“. Vyvinutý Josiah Willard Gibbs a Oliver Heaviside , vektorový počet umožnil zejména jasně formulovat James Clerk Maxwell v teorii elektromagnetismu , a také dokázal být snadné použití v klasické mechanice. Tyto úspěchy z ní učinily dodnes nejpoužívanější matematický systém ve fyzice.

Na začátku XX th století, teorie obecné relativity vede k rozpoznat časový prostor rozměru 4. Výpočet vektor nezasahuje moc v rozměru 4, jedním z důvodů je, že vektor výrobek je definován pouze v rozměru 3. Fyzici , stále nemající znalosti o algebrech objevených Cliffordem, kompenzovat nedostatky vektorového počtu zavedením různých doplňkových matematických systémů.

Teprve ve druhé polovině XX tého století David Hestenes ukázala, že geometrická algebra je naprosto dostačující co do velikosti 4, kde to přichází v algebry časoprostoru ( Space-Time Algebra ), která formalizuje a elegantně účinně speciální teorie relativity. Hestenes také ukazuje, že s geometrickou algebrou získává elektromagnetismus na jednoduchosti a že klasická mechanika v dimenzi 3 těží z lepší správy rotací. Dalším významným výsledkem, který Hestenes získal, je to, že kvantovou mechaniku lze přeformulovat geometrickou algebrou bez imaginárních čísel a bez matic s geometrickou interpretací.

Dnes jeho obhájci představují geometrickou algebru jako univerzální jazyk pro inženýry a fyziky. Jejich argumenty jsou solidní, ale váha historie je proti refoundaci, kterou navrhují, a jejich příčina postupuje jen pomalu.

Definice

Geometrická algebra

Definice - Geometrický algebry je jednotkový asociativní algebra přes pole , generované prostřednictvím vektoru podprostoru , všechny prvky vektorového prostoru, který je skalární na čtverec .

Pomocí této definice, geometrický algebry, pole a vektor podprostor jsou označovány v tomto pořadí , a . $\ mathcal {G}$ $\ mathbb {K}$ $\ mathcal {V}$

Hestenes vyjádřil svou silnou nechuť uvažovat o případu algebry nad polem komplexů. Ve skutečnosti je v Hestenes, Li a Rockwood 2001 pole skalárů skutečně vybráno stejně jako pole realů. Zde je uvedena nejobecnější definice, ale ve zbytku tohoto článku se bude předpokládat, pokud nebude uvedeno jinak . Ve stejné práci, Hestenes také ukládá do konečné dimenze $n$ . V tomto případě a lze označit jednotlivě a (nebo ). ${\ mathbb {K}} = \ mathbb {R}$ $\ mathcal {V}$ $\ mathcal {V}$ $\ mathcal {G}$ ${\ mathcal {V}} ^ {n}$ ${\ mathcal {G}} _ {n}$ ${\ mathcal {G}} ({\ mathcal {V}} ^ {n})$

V tomto článku má jakoukoli dimenzi, ale v případě, že je tato dimenze nekonečná, bude se i nadále předpokládat, že je spočítatelná pro usnadnění zápisů. $\ mathcal {V}$

Operace násobení v geometrické algebře se nazývá geometrický součin .

Euklidovský případ

Když je konečné dimenze a čtverec kteréhokoli prvku je kladný, hovoříme z důvodů oprávněných později o „euklidovském případě“. $\ mathcal {V}$ $\ mathcal {V}$

Cliffordova algebra

Data vektorového prostoru a kvadratické formy na umožňují konstrukci geometrické algebry známé jako generované pod podmínkou . Tato algebra se nazývá Cliffordova algebra . $\ mathcal {V}$ ${\ mathcal {Q}}$ $\ mathcal {V}$ $\ mathcal {V}$ $v ^ {2} = {\ mathcal {Q}} (v)$

Pokud Cliffordova algebra vyžaduje pro svou definici kvadratickou formu, uvidíme později, že naopak geometrická algebra umožňuje jednoznačně definovat kvadratickou formu z geometrického součinu. Pojem geometrické algebry je tedy totožný s pojmem Cliffordovy algebry, přičemž jediným rozdílem je pořadí prezentace: Cliffordova algebra je definována z vektorového prostoru a kvadratické formy, zatímco geometrická algebra je definována z algebry a konkrétního vektoru podprostor. To je důvod, proč mnoho zdrojů čistě a jednoduše definuje geometrické algebry jako Cliffordovy algebry, což přesně odpovídá těmto dvěma konceptům.

Vektor

I když má strukturu vektorového prostoru, David Hestenes rezervuje slovo vektor pro prvky . V tomto článku se zpravidla vektory budou zapsány v malými písmeny tučně . $\ mathcal {G}$ $\ mathcal {V}$

Neplatnost

O nulovém čtvercovém vektoru se říká, že je nula . Někdy je termín vyhrazen pro jiné vektory než nulu, tj. Vektory, které nejsou triviálně nulové.

Podpis

Podpis na nenulovou vektoru $A$ je znamením o $o 2$ .

Velikost

Velikost nebo norma vektoru $je$ označován $| a |$ , je pozitivní skutečný

{\ displaystyle | \ mathbf {a} | = {\ sqrt {| \ mathbf {a} ^ {2} |}},}

kde $| a 2 |$ označuje absolutní hodnotu reálného $a 2$ (nebo modul komplexu , v případě ). ${\ mathbb {K}} = \ mathbb {C}$

Výrobky pro vnitřní i venkovní použití

Z geometrického součinu dvou vektorů $a$ a $b$ definujeme dva nové produkty, z nichž první je symetrický a druhý antisymetrický:

{\ displaystyle {\ begin {aligned} \ mathbf {a} \ cdot \ mathbf {b} & = {\ frac {1} {2}} \ left (\ mathbf {a} \ mathbf {b} + \ mathbf { b} \ mathbf {a} \ right) \\\ mathbf {a} \ wedge \ mathbf {b} & = {\ frac {1} {2}} \ left (\ mathbf {a} \ mathbf {b} - \ mathbf {b} \ mathbf {a} \ right) \ end {zarovnáno}}}

$a • b$ se nazývá interní produkt , $a \land b$ se nazývá externí produkt . Francouzsky mluvící vědecká literatura také používá symbol $\land$ k označení $křížového$ produktu . Tato nejednoznačnost v anglosaské literatuře neexistuje, protože křížový produkt je tam označen symbolem $\times$ .

Věta - Vnitřní produkt dvou vektorů je skalární

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} \ in \ mathbb {K}}

. Demonstrace

${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ frac {1} {2}} (\ mathbf {a} \ mathbf {b} + \ mathbf {b} \ mathbf {a}) = {\ frac {1} {2}} ((\ mathbf {a} + \ mathbf {b}) ^ {2} - \ mathbf {a} ^ {2} - \ mathbf {b} ^ {2}) \ v \ mathbb {K}.}$

Externí produkt je zobecněn na $k$ vektory podle následujícího vzorce:

{\ displaystyle \ bigwedge _ {j = 1} ^ {k} \ mathbf {a} _ {j} = \ mathbf {a} _ {1} \ wedge \ mathbf {a} _ {2} \ wedge \ dots \ klín \ mathbf {a} _ {k} = {\ frac {1} {k!}} \ sum _ {\ sigma \ v {\ mathfrak {S}} _ {k}} \ operatorname {sgn} (\ sigma ) \ mathbf {a} _ {\ sigma (1)} \ mathbf {a} _ {\ sigma (2)} \ dots \ mathbf {a} _ {\ sigma (k)}}

kde je skupina permutací indexu $k$ . ${\ mathfrak {S}} _ {k}$

Priority výpočtu

Většina autorů dává interiérovým a exteriérovým produktům vyšší prioritu než geometrický produkt, takže:

{\ begin {aligned} {\ mathbf {a}} {\ mathbf {b}} \ cdot {\ mathbf {c}} = {\ mathbf {a}} ({\ mathbf {b}} \ cdot {\ mathbf {c}}) \\ {\ mathbf {a}} \ cdot {\ mathbf {b}} {\ mathbf {c}} = ({\ mathbf {a}} \ cdot {\ mathbf {b}}) { \ mathbf {c}} \\ {\ mathbf {a}} {\ mathbf {b}} \ wedge {\ mathbf {c}} = {\ mathbf {a}} ({\ mathbf {b}} \ wedge { \ mathbf {c}}) \\ {\ mathbf {a}} \ wedge {\ mathbf {b}} {\ mathbf {c}} = ({\ mathbf {a}} \ wedge {\ mathbf {b}} ) {\ mathbf {c}} \ end {zarovnáno}}

Kanonický rozklad

Pro dva vektory $a$ a $b$ máme následující vztah, který představuje takzvaný kanonický rozklad geometrického součinu dvou vektorů:

{\ displaystyle \ mathbf {ab} = \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ klín \ mathbf {b}.}

${\ mathbf {a}} \ cdot {\ mathbf {b}}$ a jsou jednotlivě nazývány (z důvodů oprávněných později ) skalární částí a bivektoriální částí geometrického součinu $ab$ . ${\ mathbf {a}} \ klín {\ mathbf {b}}$

Ortogonalita

Dva vektory, jejichž vnitřním součinem je skalární 0, jsou považovány za ortogonální .

Ortonormální základna

Rodina vektorů $( e 1 , e 2 , ...)$ se říká, že ortonormálních při:

${\ mathbf {e}} _ {i} \ cdot {\ mathbf {e}} _ {j} = \ delta _ {{ij}}$

kde skalární $δ ij$ je Kroneckerův symbol .

Když tato rodina je také generátor z říkáme, že to představuje orthonormal bázi vektorů geometrické algebry nebo s mírným zneužití jazyka, což je ortonormální bázi geometrické algebry . $\ mathcal {V}$

Uvidíme později, že v euklidovském případě se tato definice ortonormálního základu shoduje s definicí ortonormálního základu v euklidovském prostoru .

Čepel

Čepel $k$ je element geometrické algebře, který může být zapsán jako vnější produkt $k-$ lineárně nezávislých vektorů .

A_ {k} = \ bigwedge _ {{j = 1}} ^ {k} {\ mathbf {a}} _ {j}

Školní známka

Celé číslo $k$ je to, co nazýváme stupně z $A k$ .
Skaláry $( A 0 )$ , vektory $( A 1 )$ , bivektory $( A 2 )$ , trivektory $( A 3 )$ a obecně $k-$ vektory mají stupně 0, 1, 2, 3, $k$ .

Orientace

O dvou kolineárních lopatkách se říká, že mají stejnou orientaci, když je koeficient proporcionality, který je spojuje, kladný. Jinak se říká, že mají opačnou orientaci .

Jednotnost

O čepeli stupně $k$ se říká, že je jednotná (nebo jednotková ), když ji lze zapsat jako geometrický součin $k$ ortogonálních vektorů velikosti 1.

Degenerace

O čepeli se říká, že je zdegenerovaná nebo nulová, když je její geometrický čtverec nulový.

Útek

Vektory $( 1 , 2 , ..., k )$ tvoří to, co se nazývá rám ( rám , nebo báze ) sloučeniny $A k$ .

Také říkáme, že $A k$ je pseudoskalární pro tento rámec.

Dualita

Pro jakýkoli rámec $( a 1 , a 2 , ..., a k )$ je duální rámec rodinou vektorů $k$ $( a 1 , a 2 , ..., a k )$ tak, že:

{\ displaystyle \ mathbf {a} ^ {i} \ cdot \ mathbf {a} _ {j} = \ delta _ {j} ^ {i}.}

Vysoký index zde nepředstavuje geometrickou umocňování.

Bivektor, trivektor, k- vektor

Termíny bivektor, trivektor a k- vektor označují čepele stupně dva, tři a k . Nicméně, někteří autoři rozlišují K -vectors z k- -blades konstatováním, že K -vectors jsou částky z k- -blades. Tyto částky tvoří vektor podprostoru o , označený . Takže . $\ mathcal {G}$ ${\ mathcal {G}} ^ {k}$ ${\ displaystyle {\ mathcal {G}} ^ {1} = {\ mathcal {V}}}$

Bivektory a trivektory lze také kvalifikovat jako orientovanou oblast a orientovaný objem .

Projekce v platové třídě k

Podprostory tvoří přímý rozklad součtu geometrického prostoru: ${\ mathcal {G}} ^ {k}$

{\ mathcal {G}} = \ bigoplus _ {k} {\ mathcal {G}} ^ {k}

Tento rozklad je pro jednoho napsán: $M \ in {\ mathcal {G}}$

M = \ součet _ {k} \ langle M \ rangle _ {k}

tedy definování operátoru známého jako projekce ve stupni k . je popsána jako součást hodnost k, M , nebo části hodnosti k M . Rovněž je zaznamenána část stupně 0 nebo skalární část . $M \ mapsto \ langle M \ rangle _ {k}$ $\ langle M \ rangle _ {k}$ ${\ displaystyle \ langle M \ rangle}$

Výrobky pro vnitřní i venkovní použití

Tyto vnitřní a vnější produkty $r$ -vector $r$ a $s$ -vector $B$ $y$ mohou být definovány:

{\ displaystyle {\ begin {aligned} A_ {r} \ cdot B_ {s} & = \ langle A_ {r} B_ {s} \ rangle _ {| rs |} \\ A_ {r} \ klín B_ {s } & = \ langle A_ {r} B_ {s} \ rangle _ {r + s} \ end {zarovnáno}}}

Tato definice rozšiřuje definici interiérů a exteriérů definovaných výše pro vektory, to znamená pro $r = s = 1$ .

Hestenes, Li a Rockwood 2001 rovněž navrhují rekurzivní ekvivalentní definici.

Projekce a odmítnutí

Data nedegenerovaného čepele $A r$ umožňují zapsat libovolný vektor $a$ podle takzvaného ortogonálního rozkladu:

{\ displaystyle \ mathbf {a} = P_ {A_ {r}} (\ mathbf {a}) + P_ {A_ {r}} ^ {\ perp} (\ mathbf {a}) \ quad {\ rm {s }} \ quad P_ {A_ {r}} (\ mathbf {a}) = (\ mathbf {a} \ cdot A_ {r}) A_ {r} ^ {- 1} \ quad {\ rm {and}} \ quad P_ {A_ {r}} ^ {\ perp} (\ mathbf {a}) = (\ mathbf {a} \ klín A_ {r}) A_ {r} ^ {- 1}.}

$P _ {{A_ {r}}} ({\ mathbf {a}})$ a nazývají se projekce a odmítnutí . $P _ {{A_ {r}}} ^ {{\ perp}} ({\ mathbf {a}})$

Multivektorový

Prvky se nazývají multivektorové . Hestenes také někdy používá výraz směrované číslo , které lze přeložit jako směrované číslo . Zdá se však, že v posledních publikacích převládá pojem multivektor . ${\ mathcal {G}}$

Pourer

Vylévací ( versor anglicky) je multi-vektor může být psáno jako geometrický součin vektorů ne „ nula “.

Přepínač

Obousměrný přepínač je definován jako polovina obvyklého přepínače v kruhu : ${\ displaystyle A, B \ v {\ mathcal {G}}}$

{\ displaystyle A \ times B = {\ frac {1} {2}} (AB-BA).}

Obrácení

Reverze na multivector $M$ je multivector:

{\ displaystyle M ^ {\ dagger} = \ součet _ {k \ geq 0} (- 1) ^ {\ frac {k (k-1)} {2}} \ langle M \ rangle _ {k}.}

Někteří autoři používají vlnovka symbol namísto obele .

Operátor se nazývá hlavní antiautomorfismus . Jedná se o anti-automorphism algebry , jelikož $M \ mapsto M ^ {\ dagger}$ $\ mathcal {G}$

{\ displaystyle (\ mathbf {a} _ {1} \ mathbf {\ ldots} \ mathbf {a} _ {k}) ^ {\ dagger} = \ mathbf {a} _ {k} \ mathbf {\ ldots} \ mathbf {a} _ {1}.}

Involuce podle hodnosti

Involuce stupněm , nebo paritní konjugace nebo konjugaci části multivector $M$ je multivector:

{\ displaystyle M ^ {*} = \ součet _ {k \ geq 0} (- 1) ^ {k} \ langle M \ rangle _ {k}.}

Operátor je umocňování nazývá hlavní zápletka of . ${\ displaystyle M \ mapsto M ^ {*}}$ $\ mathcal {G}$

Parita

Multi-vektor je, že dokonce i pokud $M * = M$ . Říká se, že zvláštní, když $M * = - M$ .

Velikost

Velikost o multivector $M$ je pozitivní skalární:

| M | = {\ sqrt {\ sum _ {k} | \ langle M \ rangle _ {k} \ cdot \ langle M \ rangle _ {k} |}}

V konkrétním případě $k-$ vektoru tedy máme:

{\ displaystyle | A_ {k} | = {\ sqrt {| \ langle A_ {k} ^ {2} \ rangle |}},}

což rozšiřuje výše uvedenou definici pro $k = 1$ .

Standard

Velikost představuje standard geometrické algebry. Používá se proto také pojem standard .

Skalární součin

Skalární součin dvou multivektorů $M$ a $N$ je skalární částí geometrického součinu $M$ obrácením $N$ :

{\ displaystyle \ langle MN ^ {\ dagger} \ rangle = \ langle NM ^ {\ dagger} \ rangle.}

(Skalární součin dvou vektorů se rovná jejich produktu: ) ${\ displaystyle \ langle \ mathbf {a} \ mathbf {b} ^ {\ dagger} \ rangle = \ mathbf {a} \ cdot \ mathbf {b}}$

Kanonický základ

Kanonická základem je základem (viděn jako vektorový prostor), tak, že existuje ortonormální báze , ve kterých mohou být písemné prvky kanonické základě: $\ mathcal {G}$ $({\ mathbf {e}} _ {1}, {\ mathbf {e}} _ {2}, ...)$

e_ {J} = {\ mathbf {e}} _ {{\ sigma _ {1}}} {\ mathbf {e}} _ {{\ sigma _ {2}}} \ ldots {\ mathbf {e}} _ {{\ sigma _ {k}}}

kde je konečná a přísně rostoucí posloupnost kladných celých čísel. $J = (\ sigma _ {1}, \ sigma _ {2} \ ldots \ sigma _ {k})$

Hotový rozměr

Definice v této podsekci jsou platné pouze v případě, že má konečnou dimenzi $n$ . $\ mathcal {V}$

Pseudoscalar

Pseudoscalar je čepel, jejíž stupeň $n$ se rovná dimenzi prostoru. Všechny pseudoskaláře jsou navzájem více.

Jednotnost

Všechny jednotkové pseudoscalary, které jsou uvedeny , se rovnají znaménku mínus. Tato kvazi-jedinečnost ospravedlňuje notaci nezávislou na volbě vektorů , stejně jako na použití určitého členu . $Já _ {{\ sigma}}$ ${\ mathbf {\ sigma}}$

Jednotka pseudoscalar je tedy definována:

I = \ pm I _ {{\ sigma}}

Velikost

Velikost z pseudoscalar vzhledem k jednotce pseudoscalar je třeba poznamenat, s držáky, které ji obklopují, a je definován jako součin pseudoscalar posuzovaném inverzní jednotky pseudoscalar:

{\ displaystyle [P] = PI ^ {- 1}}

Dualita

Dvojí z multivector $M$ je:

{\ displaystyle {\ widetilde {M}} = M ^ {\ sim} = MI ^ {- 1}.}

Stejně jako unitární pseudoskal je duál definován pouze se znaménkem blízko.

Průsečík

Křižovatka ( setkají v angličtině) dvou multivectors je:

{\ displaystyle M \ vee N = {\ widetilde {M}} \ cdot N.}

Lineární transformace

Obecně jsou lineární transformace označeny podtrženým nebo podtrženým symbolem. ${\ mathcal V}$

Je důležité mít na paměti, že lineární transformace není součástí geometrické algebry. Výraz jako například proto neoznačuje geometrický součin, ale aplikaci lineární funkce na $a$ . $\ podtržení {f} {\ mathbf {a}}$ $\ podtrhnout {f}$

Asistent endomorfismu

Pro jakékoliv endomorphism části , tam je jedinečný endomorphism z taková, že: $\ podtrhnout {f}$ $\ mathcal {V}$ $\ overline f$ $\ mathcal {V}$

{\ displaystyle \ forall (\ mathbf {a}, \ mathbf {b}) \ in {\ mathcal {V}} ^ {2}, \ quad \ mathbf {a} \ cdot {\ podtržení {f}} \ mathbf {b} = \ mathbf {b} \ cdot {\ overline {f}} \ mathbf {a}.}

$\ overline f$ Potom se nazývá mimořádným endomorphism o . $\ podtrhnout {f}$

Ektomorfismus

Jakékoli endomorphism na lze samozřejmě rozšířena o : $\ podtrhnout {f}$ $\ mathcal {V}$ $\ mathcal {G}$

\ podtržení {f} (A \ klín B) = \ podtržení {f} (A) \ klín \ podtržení {f} (B)

Toto rozšíření se nazývá ektomorfismus , vzhledem k tomu, že zachovává vnější produkt.

Totéž pro jakoukoli čepel : $A_ {k} = \ bigwedge _ {{j = 1}} ^ {k} {\ mathbf {a}} _ {j}$

\ underline {f} (A_ {k}) = \ bigwedge _ {{j = 1}} ^ {k} \ underline {f} ({\ mathbf {a}} _ {j})

Linearita pak umožňuje rozšířit se na všechno . $\ podtrhnout {f}$ $\ mathcal {G}$

Pojem přídavného endomorfismu lze zobecnit na ektomorfismy vztahem:

\ langle A \ underline {f} B \ rangle = \ langle B \ overline {f} A \ rangle

Ortogonální transformace

Lineární transformace $U$ se říká, že je ortogonální, když zachovává vnitřní produkt:

${\ displaystyle \ forall (\ mathbf {a}, \ mathbf {b}) \ in ({\ mathcal {V}}) ^ {2}, \ quad ({\ podtržení {U}} \ mathbf {a}) \ cdot ({\ underline {U}} \ mathbf {b}) = \ mathbf {a} \ cdot \ mathbf {b}.}$

Tato definice je ekvivalentní následující charakterizaci:

{\ displaystyle {\ underline {U}} ^ {- 1} = {\ overline {U}}.}

Kanonická forma

Lineární transformace $U$ je ortogonální tehdy a jen tehdy, když existuje nalévač $U$ takový, že:

{\ displaystyle \ forall \ mathbf {a} \ in {\ mathcal {V}}, \ quad {\ podtržení {U}} \ mathbf {a} = U \ mathbf {a} (U ^ {*}) ^ { -1} = U ^ {*} \ mathbf {a} U ^ {- 1}.}

Toto je takzvaná kanonická forma ortogonální transformace.

Multivektorová analýza

Stejně jako data vektorového prostoru umožňují vektorovou analýzu , tj. Studium nekonečně malého počtu funkcí definovaných v tomto vektorovém prostoru se skalárními nebo vektorovými hodnotami , umožňují data geometrické algebry, jejíž prvky se nazývají multivektorové , tzv. Multivektorální analýza definovaných funkcí, ale s hodnotami tentokrát potenciálně multivektorálními. Anglosasové, stejně jako Hestenes, hovoří o geometrickém počtu nebo multivektorovém počtu , stejně jako o vektorovém počtu, aby označili to, co francouzští mluvčí nazývají vektorovou analýzou . $\ mathcal {V}$

Vektorová derivace

Nejdůležitějším nástrojem pro tuto disciplínu je pravděpodobně takzvaný vektorový derivační operátor , který lze definovat jako:

${\ displaystyle {\ begin {pole} {rccl} \ částečné: & {\ mathcal {G}} ^ {\ mathcal {V}} & \ rightarrow & {\ mathcal {G}} ^ {\ mathcal {V}} \\ & F & \ mapsto & \ left (\ mathbf {x} \ mapsto \ sum _ {j} \ mathbf {e} ^ {j} \ lim _ {\ epsilon \ rightarrow 0} {\ frac {F (\ mathbf {x} + \ epsilon \ mathbf {e} _ {j}) - F (\ mathbf {x})} {\ epsilon}} \ right) \ end {pole}}}$

Tato definice je nejčastěji poznamenal $\partial = e j \partial j$ pomocí Einsteinovy sumační konvenci . Velmi často se používá také symbol $\nabla$ .

\ nabla = {\ mathbf {e}} ^ {j} \ částečné _ {j}

Ukazuje se (srov. „ Geometrická analýza “), že tato definice má význam, pokud výraz $e j \partial j$ tvoří operátor, který nezávisí na zvolené základně.

Někteří autoři nazývají tento operátor gradient .

Vlastnosti

Symetrie a antisymetrie výrobků pro interiér a exteriér

Vnitřní a vnější produkty dvou vektorů jsou konstrukčně symetrické a antisymetrické :

{\ begin {aligned} {\ mathbf {a}} \ cdot {\ mathbf {b}} & = {\ mathbf {b}} \ cdot {\ mathbf {a}} \\ {\ mathbf {a}} \ klín {\ mathbf {b}} & = - {\ mathbf {b}} \ klín {\ mathbf {a}} \ end {zarovnáno}}

Obecněji je externí produkt několika vektorů antisymetrický:

\ forall \ sigma \ in {\ mathfrak {S}} _ {k}, \ quad \ bigwedge _ {{j = 1}} ^ {k} {\ mathbf {a}} _ {j} = \ operatorname {sgn } (\ sigma) \ bigwedge _ {{j = 1}} ^ {k} {\ mathbf {a}} _ {{sigma (j)}}

Algebraická charakterizace geometrických představ

Kollinearita a ortogonalita

Věta - Dva vektory jsou kolineární právě tehdy, je-li jejich externí součin nulový.

Demonstrace

Pokud jsou dva vektory a jsou kolineární, pak existuje skalární takové, že . Od té doby máme . ${\ mathbf {a}}$ $\ mathbf {b}$ $\ lambda$ ${\ mathbf {a}} = \ lambda {\ mathbf {b}}$ ${\ mathbf {a}} \ wedge {\ mathbf {b}} = \ lambda {\ mathbf {a}} \ wedge {\ mathbf {a}} = \ lambda 0 = 0$

Naopak, pokud , pak kanonický rozklad dává . Vynásobením pravice o to přijde, a proto ignoruje zvrhlý případ, kdy : ${\ mathbf {a}} \ klín {\ mathbf {b}} = 0$ ${\ mathbf {a}} {\ mathbf {b}} = {\ mathbf {a}} \ cdot {\ mathbf {b}}$ $\ mathbf {b}$ ${\ mathbf {a}} {\ mathbf {b}} ^ {2} = ({\ mathbf {a}} \ cdot {\ mathbf {b}}) {\ mathbf {b}}$ ${\ mathbf {b}} ^ {2} = 0$

${\ displaystyle \ mathbf {a} = {\ frac {\ mathbf {a} \ cdot \ mathbf {b}} {\ mathbf {b} ^ {2}}} \ mathbf {b}.}$

Zbývá pozorovat, že jde o skalár jako podíl dvou skalárů. Existuje tedy skutečně kolineárnost. ${\ frac {{\ mathbf {a}} \ cdot {\ mathbf {b}}} {{\ mathbf {b}} ^ {2}}}$

Toto pozorování, přidané k definici ortogonality, nám umožňuje odvodit následující dvě základní vlastnosti:

Algebraická charakterizace ortogonality a kolinearity -

Dva vektory jsou ortogonální, právě když jsou proti dojíždění.
Dva vektory jsou kolineární právě tehdy, když dojíždějí.

To znamená:

{\ begin {array} [t] {ccccc} {\ mathbf {a}} \ perp {\ mathbf {b}} & \ iff & {\ mathbf {a}} \ cdot {\ mathbf {b}} = 0 & \ iff & {\ mathbf {a}} {\ mathbf {b}} = - {\ mathbf {b}} {\ mathbf {a}} \\ {\ mathbf {a}} \ propto {\ mathbf {b }} & \ iff & {\ mathbf {a}} \ wedge {\ mathbf {b}} = 0 & \ iff & {\ mathbf {a}} {\ mathbf {b}} = {\ mathbf {b}} {\ mathbf {a}} \ end {pole}}

Lineární nezávislost

Zobecnění algebraické charakterizace kolinearity existuje pro lineární nezávislost . Ve skutečnosti jsou vektory lineárně nezávislé právě tehdy, když jejich externí produkt není nula. Nebo ekvivalentním způsobem jsou lineárně závislé právě tehdy, když je jejich externí produkt nulový: $k$ $({\ mathbf {a}} _ {1}, {\ mathbf {a}} _ {2} \ ldots, {\ mathbf {a}} _ {k})$

{\ displaystyle \ left (\ existuje (\ alpha _ {1}, \ alpha _ {2} \ ldots, \ alpha _ {k}) \ in \ mathbb {K} ^ {k} \ setminus \ {(0, \ ldots, 0) \} \ quad \ sum _ {j} \ alpha _ {j} \ mathbf {a} _ {j} = 0 \ right) \ iff \ bigwedge _ {j = 1} ^ {k} \ mathbf {a} _ {j} = 0.}

Vektorové podprostory

Pro podprostoru o rozměru , že je čepel $r$ taková, že: ${\ mathcal {F}}$ ${\ mathcal V}$ $r$

{\ displaystyle \ forall \ mathbf {x} \ in {\ mathcal {V}} \ quad {\ bigl (} \ mathbf {x} \ in {\ mathcal {F}} \ iff \ mathbf {x} \ klín A_ {r} = 0 {\ bigr)}.}

Každá čepel $r$ tedy charakterizuje vektor podprostoru, který se poté, že se svírá , generovány nebo režie od $A$ $r$ .

V konkrétním případě, kdy má konečný rozměr, přichází: ${\ mathcal V}$ ${\ displaystyle \ forall \ mathbf {x} \ in {\ mathcal {V}} \ quad \ mathbf {x} \ klín I = 0.}$

Jacobi Identita

{\ displaystyle A \ times (B \ times C) = (A \ times B) \ times C + B \ times (A \ times C).}

Pozoruhodné struktury

Kvadratický prostor

Vzhledem k tomu, interiér součin dvou vektorů je skalární a je distribuční a symetrické, to představuje kvadratickou formu na a tak dává Vektory geometrické algebře s přirozenou kvadratickou strukturu . $\ mathcal {V}$

V případě definovaném dříve jako euklidovský je součin interiéru definován také kladně, a proto splňuje nezbytné a dostatečné podmínky pro definování skalárního součinu , čímž se kvadratická struktura stává euklidovským, odtud název „euklidovský případ“. V tomto případě se dříve definované pojmy normy a ortogonality shodují s pojmy euklidovské normy a ortogonality v euklidovském smyslu.

Externí algebra

Externí Produkt poskytuje ( zapomenutí geometrickou produkt, z něhož pochází) alternativní definici vnější algebry z : $\ mathcal {V}$

{\ displaystyle \ wedge {\ mathcal {V}} = {\ mathcal {G}} \ quad {\ rm {auto}} \ quad {\ mathcal {G}} = \ bigoplus _ {k} {\ mathcal {G }} ^ {k} \ quad {\ rm {et}} \ quad {\ mathcal {G}} ^ {k} = \ klín ^ {k} {\ mathcal {V}}.}

Slovník geometrické algebry se proto překrývá se slovy externích algeber. Například snímek stupně se také nazývá multivektor stupně $k$ , $k$ -multivector nebo dokonce $k$ -vector . $k$

Složité subalgebry

Čtverec libovolného bivektoru jednotky $( e 1 e 2 )$ vytvořeného ze dvou vektorů se stejnými podpisy se rovná –1:

{\ displaystyle \ mathbf {e} _ {1} ^ {2} \ mathbf {e} _ {2} ^ {2} = 1 \ Rightarrow (\ mathbf {e} _ {1} \ mathbf {e} _ { 2}) ^ {2} = - 1.}

Proto podalgebry generované dvojice $(1, e 1 e 2 ),$ je pole izomorfní se oboru komplexů. Tento izomorfismus pak ospravedlňuje notaci:

i = {\ mathbf {e}} _ {1} {\ mathbf {e}} _ {2}

takže máme:

{\ displaystyle i ^ {2} = - 1.}

Tento výsledek lze ve skutečnosti zobecnit na všechny lopatky jednotek, jejichž čtverec se rovná -1. Každý generuje s jednotnou čepelí nultého stupně tělo izomorfní s tělem komplexů. To je například případ unitárního pseudoskaláře v euklidovském případě dimenze 3:

{\ displaystyle I ^ {2} = - 1.}

Posuv jednotek 1. stupně, tj. Jednotkový vektor, může také generovat tělo izomorfní s tělem komplexů. Je nezbytné a dostačující, aby byl jeho podpis negativní. To platí zejména v případě, kdy kvadratická struktura není euklidovská, ale Lorentzianova . Navíc, když existují alespoň dva vektory s různými podpisy, je možné sestrojit bivektor jednotky $j$ tak, že $j 2 = +1$ , a subalgebra, kterou generuje s jednotkou, je pak izomorfní s polem vytvořených komplexních čísel , dávat podprostor odpovídající geometrické struktury hyperbolický .

Čtveřice

V konkrétním případě, kde $n = 3$ , lze vytvořit tři bivektory jednotek: ${\ displaystyle i = \ mathbf {e} _ {1} \ mathbf {e} _ {2}, \ quad j = \ mathbf {e} _ {2} \ mathbf {e} _ {3} \ quad {\ rm {et}} \ quad k = \ mathbf {e} _ {1} \ mathbf {e} _ {3}.}$

V euklidovském případě máme také:

${\ displaystyle i ^ {2} = j ^ {2} = k ^ {2} = ijk = -1,}$

takže subalgebra generovaná $(1, i , j , k )$ je izomorfní s polem čtveřic .

$i$ , $j$ a $k$ nejsou přesně jednotkové bivektory přirozeně generované ortonormálním základem. Ve skutečnosti máme $i = e 1 e 2$ , $j = e 2 e 3$ , ale na druhé straně $k = - e 3 e 1$ . Richard Wareham ve své disertační práci zmiňuje tento rozdíl a vidí jej jako příčinu určitých chyb ve znamení, které se někdy objevují při použití čtveřic. Tomuto tématu se věnuje také Chris Doran.

Lež algebra

${\ mathcal {G}} ^ {2}$ je stabilní pomocí přepínačů. Jako takový a vzhledem k identitě Jacobiho tvoří lži algebry .

Reverzibilita

Geometrická algebra zdědila ze své jednotné prstencové struktury pojem inverze : prvek $A$ se říká, že je invertibilní, pokud existuje prvek $A -1$ ( který je pak jedinečný ) takový, že

{\ displaystyle AA ^ {- 1} = A ^ {- 1} A = 1.}

Každý ne nulový vektor z nezvratné: $\ mathcal {V}$

{\ displaystyle \ mathbf {a} ^ {- 1} = {\ frac {\ mathbf {a}} {\ mathbf {a} ^ {2}}}.}

Pourers jsou proto invertible, jako produkty invertibles :

{\ displaystyle A ^ {- 1} = {\ frac {A ^ {\ dagger}} {A ^ {\ dagger} A}}.}

De Morganovo pravidlo

{\ displaystyle (A \ vee B) ^ {\ sim} = {\ widetilde {A}} \ wedge {\ widetilde {B}}.}

Pozoruhodné identity

Mezi tyto pozoruhodné identity jsou uvedeny v McDonald 2015 . Ne všechny jsou vzneseny kvůli mírně odlišným hodnocením.

${\ displaystyle {\ begin {zarovnáno} A \ cdot (B \ cdot C) & = (A \ klín B) \ cdot C \\ (\ mathbf {a} \ klín \ mathbf {b}) \ cdot (\ mathbf {c} \ wedge \ mathbf {d}) & = (\ mathbf {a} \ cdot \ mathbf {d}) (\ mathbf {b} \ cdot \ mathbf {c}) - (\ mathbf {a} \ cdot \ mathbf {c}) (\ mathbf {b} \ cdot \ mathbf {d}) \\\ mathbf {a} \ cdot (\ mathbf {bc}) & = (\ mathbf {a} \ cdot \ mathbf {b }) \ mathbf {c} - (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b} \\\ mathbf {a} \ cdot (\ mathbf {b} \ klín \ mathbf {c}) & = (\ mathbf {a} \ cdot \ mathbf {b}) \ mathbf {c} - \ mathbf {b} (\ mathbf {a} \ cdot \ mathbf {c}) \ end {zarovnáno}}}$

Propojte s křížovým produktem

Vnější součin $a \land b$ není ani skalární, ani vektor: je to bivektor , který bude později identifikován jako dvojník vektoru , který je výsledkem křížového součinu . Rozdíl mezi těmito dvěma operacemi spočívá v tom, že bivektor poskytovaný externím produktem je vlastní rovině dvou vektorů, zatímco křížový produkt je označován jako pseudovektor kolmý na tuto rovinu.

Vnější produkt dvou vektorů lze považovat za orientovanou oblast .

Geometrická interpretace

Jednotkové bivektory

Jednotkový bivektor $s$ je geometrický součin dvou ortonormálních vektorů, které můžeme, aniž bychom ztratili obecnost , považovat za první dva vektory ortonormálního základu $( e 1 , e 2 , ...)$ :

s = {\ mathbf {e}} _ {1} {\ mathbf {e}} _ {2}

Ortonalita $e 1$ a $e 2$ dává mimo jiné:

s = {\ mathbf {e}} _ {1} {\ mathbf {e}} _ {2} = {\ mathbf {e}} _ {1} \ wedge {\ mathbf {e}} _ {2} = - {\ mathbf {e}} _ {2} \ wedge {\ mathbf {e}} _ {1} = - {\ mathbf {e}} _ {2} {\ mathbf {e}} _ {1}

Pozoruhodný charakter $s$ pochází ze skutečnosti, že geometrický součin podle $s$ ponechává vektorový prostor generovaný $($ $e$ $1$ $,$ $e$ $2$ $, ...)$ stabilní , a proto definuje lineární transformaci (nebo přesněji dvě lineární transformace, v závislosti na ať už se násobení odehrává vpravo nebo vlevo), což umožňuje přímou geometrickou interpretaci:

${\ displaystyle {\ begin {aligned} (\ alpha \ mathbf {e} _ {1} + \ beta \ mathbf {e} _ {2}) s = & (\ alpha \ mathbf {e} _ {1} ^ {2}) \ mathbf {e} _ {2} & - (\ beta \ mathbf {e} _ {2} ^ {2}) \ mathbf {e} _ {1} \\ s (\ alpha \ mathbf { e} _ {1} + \ beta \ mathbf {e} _ {2}) = & (- \ alpha \ mathbf {e} _ {1} ^ {2}) \ mathbf {e} _ {2} & + (\ beta \ mathbf {e} _ {2} ^ {2}) \ mathbf {e} _ {1} \ end {zarovnáno}}}$

Důležitým bodem je, že $th 21$ a $e 22$ jsou skalární kvůli kritériu kontrakce.

Čtverec $s$ je skalární, protože

{\ displaystyle s ^ {2} = - \ mathbf {e} _ {1} ^ {2} \ mathbf {e} _ {2} ^ {2}.}

Je záporné, pokud mají $e 1$ a $e 2$ stejný podpis, a kladné jinak. Algebraické chování (a geometrické v rovině $( e 1 , e 2 , ...)$ ) $s$ je radikálně odlišné ve dvou případech.

Euklidovský případ

Když mají $e 1$ a $e 2$ stejný podpis, máme buď nebo . V obou případech má bivektor $e$ $1$ $e$ $2$ stejné algebraické a geometrické vlastnosti, ale pro opravu myšlenek, které zde vybereme , tj. Euklidovský případ. ${\ displaystyle \ mathbf {e} _ {1} ^ {2} = \ mathbf {e} _ {2} ^ {2} = + 1}$ ${\ mathbf {e}} _ {1} ^ {2} = {\ mathbf {e}} _ {2} ^ {2} = - 1$ ${\ displaystyle \ mathbf {e} _ {1} ^ {2} = \ mathbf {e} _ {2} ^ {2} = + 1}$

Pak máme důležitou vlastnost , to znamená: $s ^ {2} = - {\ mathbf {e}} _ {1} ^ {2} {\ mathbf {e}} _ {2} ^ {2} = - 1$

{\ displaystyle s ^ {2} = - 1.}

$s$ pak generuje s jednotou subalgebra isomorfní s polem komplexů, jak je vidět výše. To od této chvíle navrhuje používat v této části písmeno $i$ místo $s$ .

Budeme mít také následující vztahy:

{\ begin {aligned} i {\ mathbf {e_ {1}}} & = - {\ mathbf {e_ {2}}} \\ i {\ mathbf {e_ {2}}} & = {\ mathbf {e_ {1}}} \ end {zarovnáno}}

{\ begin {aligned} {\ mathbf {e_ {1}}} i & = {\ mathbf {e_ {2}}} \\ {\ mathbf {e_ {2}}} i & = - {\ mathbf {e_ {1}}} \ end {zarovnáno}}

To znamená, že násobení $i$ přemění jakýkoliv lineární kombinace a $( e 1 , e 2 , ...)$ o čtvrtinu otáčky ve směru, který závisí na straně, na které se provádí násobení (doleva nebo doprava ). Můžeme zajistit, aby rotace byla o čtvrtinu otáčky, například tím, že si všimneme, že 4 je nejmenší celé číslo $k$ takové, že $i k = 1$ . Ukazuje se, že tato čtvrtotáčková rotace generuje skupinu rotací, jak je znázorněno níže.

Geometrický součin dvojice jednotkových vektorů je označen $U$ a nazývá se obraceč : ${\ displaystyle \ mathbf {a}, \ mathbf {b} \, (| \ mathbf {a} | = | \ mathbf {b} | = 1) \,}$

U = {\ mathbf {ab}}

Jméno obracečka je odůvodněn tím, že transformuje a $b$ směrem k sobě prostřednictvím otáčení: $U$

{\ displaystyle \ mathbf {b} = \ mathbf {a} U, \ quad \ mathbf {a} = U \ mathbf {b}}

Když jsou $a$ a $b$ v rovině $( e 1 , e 2 , ...)$ , můžeme bez ztráty obecnosti zvolit $e 1 = a$ a najít úhel $θ$ takový, že:

{\ mathbf {b}} = \ cos (\ theta) {\ mathbf {e}} _ {1} + \ sin (\ theta) {\ mathbf {e}} _ {2}

$U$ se pak píše:

${\ displaystyle U = \ mathbf {ab} = \ cos (\ theta) \ mathbf {e} _ {1} \ mathbf {e} _ {1} + \ sin (\ theta) \ mathbf {e} _ {1 } \ mathbf {e} _ {2} = \ cos (\ theta) + \ sin (\ theta) \ mathbf {e} _ {1} \ mathbf {e} _ {2}}$

a proto spojením skalární a bivektoriální části kanonického rozkladu:

{\ begin {aligned} {\ mathbf {a}} \ cdot {\ mathbf {b}} & = \ cos (\ theta) \\ {\ mathbf {a}} \ klín {\ mathbf {b}} & = i \ sin (\ theta) \ end {zarovnáno}}

kde $i$ je jednotkový bivektor:

{\ displaystyle i = \ mathbf {e} _ {1} \ mathbf {e} _ {2} = {\ frac {\ mathbf {a} \ klín \ mathbf {b}} {\ sin (\ theta)}} = {\ frac {U- \ cos (\ theta)} {\ sin (\ theta)}}.}

Pak je možné napsat:

${\ displaystyle U = U _ {\ theta} = \ mathbf {ab} = \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ klín \ mathbf {b} = \ cos (\ theta) + i \ sin (\ theta) = e ^ {i \ theta},}$

to znamená:

{\ displaystyle U _ {\ theta} = e ^ {i \ theta}.}

Když vynásobíme (například nalevo) tento obraceč vektorem $x ( ϕ )$ tak, že:

${\ displaystyle \ mathbf {x} (\ phi) = \ cos (\ phi) \ mathbf {e} _ {1} + \ sin (\ phi) \ mathbf {e} _ {2}}$

získáme aplikací trigonometrických identit a algebraických pravidel ortonormality $e 1$ a $e 2$ :

${\ displaystyle {\ begin {zarovnáno} \ mathbf {x} (\ phi) U _ {\ theta} & = \ mathbf {x} (\ phi) e ^ {i \ theta} \\ & = (\ cos ( \ phi) \ mathbf {e} _ {1} + \ sin (\ phi) \ mathbf {e} _ {2}) (\ cos (\ theta) + i \ sin (\ theta)) \\ & = \ cos (\ phi) \ mathbf {e} _ {1} \ cos (\ theta) + \ sin (\ phi) \ mathbf {e} _ {2} \ cos (\ theta) + \ cos (\ phi) \ mathbf {e} _ {1} i \ sin (\ theta) + \ sin (\ phi) \ mathbf {e} _ {2} i \ sin (\ theta) \\ & = (\ cos (\ phi) \ cos (\ theta) - \ sin (\ phi) \ sin (\ theta)) \ mathbf {e} _ {1} + (\ cos (\ theta) \ sin (\ phi) + \ cos (\ phi) \ sin (\ theta)) \ mathbf {e} _ {2} \\ & = \ cos (\ phi + \ theta) \ mathbf {e} _ {1} + \ sin (\ phi + \ theta) \ mathbf { e} _ {2} \\ & = \ mathbf {x} (\ phi + \ theta). \ End {zarovnáno}}}$

Vektor $x ( ϕ )$ se proto „otočil“ o úhel $θ$ . Podobný výpočet by ukázal, že pravé násobení otočí $x ( ϕ )$ o úhel $-θ$ .

Celkem :

{\ displaystyle {\ begin {aligned} \ mathbf {x} (\ phi) U _ {\ theta} & = \ mathbf {x} (\ phi + \ theta) \\ U _ {\ theta} \ mathbf {x } (\ phi) & = \ mathbf {x} (\ phi - \ theta). \ end {zarovnáno}}}

Geometrický součin dvou jednotkových vektorů proto představuje rotaci.

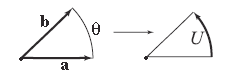
Mezi obracečem a vektorem existuje analogie.

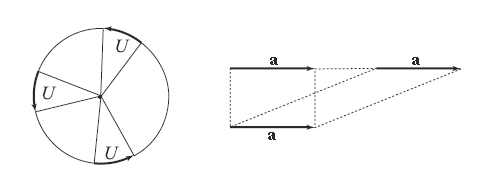
Složení rotace bude vyjádřeno součinem dvou obracečů:

U _ {{\ theta}} U _ {{\ varphi}} = U _ {{\ theta + \ varphi}}

Je užitečné poznamenat, že:

U _ {{\ varphi}} {\ mathbf {x}} (\ phi) U _ {{\ psi}} = U _ {{\ varphi}} {\ mathbf {x}} (\ phi + \ psi) = {\ mathbf {x}} (\ phi + \ psi - \ varphi)

a to tedy pro $ϕ = - θ / 2$ a $ψ = θ / 2$ :

{\ displaystyle U _ {- {\ frac {\ theta} {2}}} \ mathbf {x} (\ phi) U _ {\ frac {\ theta} {2}} = \ mathbf {x} (\ phi + \ theta)}

To představuje tzv. Kanonickou formulaci rotace úhlu $θ$ .

Minkowského prostor

Když mají $e 1$ a $e 2$ jiný podpis (řekněme například k opravě nápadů, to a ), máme , to znamená: ${\ mathbf {e}} _ {1} ^ {2} = 1$ ${\ mathbf {e}} _ {2} ^ {2} = - 1$ $s ^ {2} = - {\ mathbf {e}} _ {1} ^ {2} {\ mathbf {e}} _ {2} ^ {2} = 1$

s ^ {2} = 1

Násobení $y$ swap $e 1$ a $e 2$ :

{\ mathbf {e}} _ {1} s = {\ mathbf {e}} _ {1} {\ mathbf {e}} _ {1} {\ mathbf {e}} _ {2} = {\ mathbf {e}} _ {1} ^ {2} {\ mathbf {e}} _ {2} = {\ mathbf {e}} _ {2}

{\ displaystyle \ mathbf {e} _ {2} s = \ mathbf {e} _ {2} \ mathbf {e} _ {1} \ mathbf {e} _ {2} = - \ mathbf {e} _ { 2} \ mathbf {e} _ {2} \ mathbf {e} _ {1} = - \ mathbf {e} _ {2} ^ {2} \ mathbf {e} _ {1} = \ mathbf {e} _ {1},}

to znamená:

{\ begin {aligned} {\ mathbf {e}} _ {1} s & = {\ mathbf {e}} _ {2} \\ {\ mathbf {e}} _ {2} s & = {\ mathbf {e}} _ {1} \ end {zarovnáno}}

{\ displaystyle {\ begin {aligned} s \ mathbf {e} _ {1} & = - \ mathbf {e} _ {2} \\ s \ mathbf {e} _ {2} & = - \ mathbf {e } _ {1}. \ Konec {zarovnáno}}}

Násobení $s$ tedy působí v rovině $( e 1 , e 2 , ...)$ jako odraz, jehož osa je jedním z půlících čar přímek směrovaných $e 1$ a $e 2$ , volba půlící čáry v závislosti na straně kde se provádí množení (vpravo nebo vlevo).

Skutečnost, že $s 2 = 1$ odpovídá involutivní povaze odrazů.

Násobení odlévatelem

Pokud nebude uvedeno jinak, odsud se omezíme na euklidovský případ.

Obecný případ

Nyní považujeme pár vektorů $( a , b ) za$ ne nutně jednotný, ale ne nulový a ne kolineární. Předchozí výsledky lze zobecnit zvážením páru:

({\ mathbf {{\ tilde {a}}}}, {\ mathbf {{\ tilde {b}}}}) = ({\ frac {{\ mathbf {a}}} {| {\ mathbf {a }} |}}, {\ frac {{\ mathbf {b}}} {| {\ mathbf {b}} |}})

Vektory a jsou samy jednotné a mají stejné podpisy jako $a$ a $b$ . Jsou také odděleny stejným úhlem $θ$ , takže je obraceč zapsán: ${\ mathbf {{\ tilda a}}}$ ${\ mathbf {{\ tilda b}}}$ ${\ mathbf {{\ tilde {a}}}} {\ mathbf {{\ tilde {b}}}}$

{\ mathbf {{\ tilde {a}}}} {\ mathbf {{\ tilde {b}}}} = e ^ {{i \ theta}}

nebo

{\ displaystyle i = {\ frac {\ mathbf {\ tilde {a}} \ klín \ mathbf {\ tilde {b}}} {\ sin (\ theta)}}}

Geometrický součin lze tedy psát:

{\ mathbf {a}} {\ mathbf {b}} = | {\ mathbf {a}} || {\ mathbf {b}} | e ^ {{i \ theta}}

zatímco bivektor jednotky $i$ lze zapsat:

{\ displaystyle i = {\ frac {\ mathbf {a} \ klín \ mathbf {b}} {| \ mathbf {a} || \ mathbf {b} | \ sin (\ theta)}}.}

Dříve jsme viděli, že množina multivektorů generovaných - lineárními kombinacemi a geometrickými součiniteli - 1 a $i$ je pole izomorfní vůči poli komplexních čísel. To ospravedlňuje použití podobné slovní zásoby a notací.

Takže pokud označíme $Z$ produktové $ab$ , skalární

| z | = | {\ mathbf {a}} {\ mathbf {b}} | = | {\ mathbf {a}} || {\ mathbf {b}} |

je to, co nazýváme modulem $z$ . Toto je velmi odlišná představa od výše zmíněné normy (nebo kvantity), protože ta je definována pouze pro vektory a $z$ není vektor.

Stejně jako lze složité číslo rozložit na skutečnou část a imaginární část, lze geometrický součin rozložit na dvě části, které nejsou větší ani menší než vnitřní a vnější součin, který lze také nazvat symetrickým a antisymetrickým nebo skalárním. a bivektoriální .

{\ displaystyle {\ začátek {zarovnáno} z & = \ mathbf {a} \ cdot \ mathbf {b} & + & \ mathbf {a} \ klín \ mathbf {b} \\ & = | z | \ cos (\ theta) & + & | z | i \ sin (\ theta). \ end {zarovnáno}}}

Podobně $θ$ může být nazýván argumentu z $Z$ .

$z$ lze interpretovat geometricky jako orientovaný oblouk kruhu o poloměru $z$ .

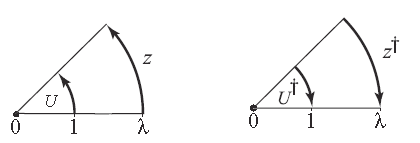
Konjugát $z$ je multivektor se stejnou skalární částí, ale s opačnou bivektorickou složkou:

z ^ {{\ dagger}} = ({\ mathbf {ab}}) ^ {{\ dagger}} = {\ mathbf {a}} \ cdot {\ mathbf {b}} - {\ mathbf {a}} \ wedge {\ mathbf {b}} = {\ mathbf {b}} \ cdot {\ mathbf {a}} + {\ mathbf {b}} \ wedge {\ mathbf {a}} = {\ mathbf {ba} }

Konjugát geometrického součinu se proto jeví jako geometrický součin prováděný v opačném pořadí:

{\ displaystyle (\ mathbf {ab}) ^ {\ dagger} = \ mathbf {ba}.}

Tuto skutečnost lze použít k výpočtu modulu geometrického součinu $z$ .

$| zz ^ {{\ dagger}} | = | {\ mathbf {a}} {\ mathbf {b}} {\ mathbf {b}} {\ mathbf {a}} | = | {\ mathbf {a}} ^ {2} {\ mathbf {b}} ^ {2} | = | {\ mathbf {a}} | ^ {2} | {\ mathbf {b}} | ^ {2} = | z | ^ {2 }$

jinými slovy :

{\ displaystyle | z | = {\ sqrt {| zz ^ {\ dagger} |}}.}

Geometrické produkty lze použít přímo na vektory:

{\ mathbf {b}} = {\ mathbf {a}} ^ {{- 1}} z = z ^ {{\ dagger}} {\ mathbf {a}} ^ {{- 1}}

s inverzí vektoru $je$ dán vztahem

{\ displaystyle \ mathbf {a} ^ {- 1} = {\ frac {1} {\ mathbf {a}}} = {\ frac {\ mathbf {a}} {\ mathbf {a} ^ {2}} } = {\ frac {\ mathbf {a}} {| \ mathbf {a} | ^ {2}}}.}

Zde se geometrický součin $z$ otáčí na vektoru $a$ mění $jeho$ měřítko, aby získal vektor $b$ (to je podobnost ).

Euklidovský prostor dimenze 3

Dovolit být euklidovský vektorový prostor . Násobením a sčítáním vektory generují geometrickou algebru . Zejména můžeme vytvořit základ pro geometrické algebře z kanonické ortonormální báze z . ${\ mathcal {P}} ^ {3}$ ${\ mathcal {G}} _ {3} = {\ mathcal {G}} \ vlevo ({\ mathcal {P}} ^ {3} \ vpravo)$ $\ lbrace {\ mathbf {\ sigma _ {1}}}, {\ mathbf {\ sigma _ {2}}}, {\ mathbf {\ sigma _ {3}}} \ rbrace$ ${\ mathcal {P}} ^ {3}$

Pomocí geometrického součinu můžeme definovat pseudoskalární jednotku (která představuje orientovaný objem):

{\ displaystyle i = \ mathbf {\ sigma _ {1}} \ mathbf {\ sigma _ {2}} \ mathbf {\ sigma _ {3}}.}

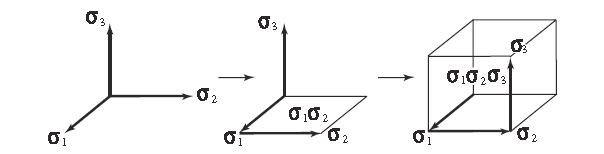
Máme také následující bivektorovou základnu

{\ mathbf {\ sigma _ {1}}} {\ mathbf {\ sigma _ {2}}} = i {\ mathbf {\ sigma _ {3}}}, \, {\ mathbf {\ sigma _ {2 }}} {\ mathbf {\ sigma _ {3}}} = i {\ mathbf {\ sigma _ {1}}}, \, {\ mathbf {\ sigma _ {3}}} {\ mathbf {\ sigma _ {1}}} = i {\ mathbf {\ sigma _ {2}}}

Jednotkové bivektory představují orientované oblasti.

Pseudoscalar $i$ má speciální vlastnosti, které usnadňují přechod mezi euklidovským vektorovým prostorem a geometrickou algebrou. My máme :

i ^ {2} = - 1

Každý bivector $B$ z je dvojí vektoru $b$ ohledem na vztah: ${\ mathcal {G}} _ {3}$

{\ mathbf {B}} = i {\ mathbf {b}} = {\ mathbf {b}} i

Operace geometrické duality je tedy jednoduše vyjádřena násobením pseudoskalárním $i$ . To umožňuje napsat externí produkt v této podobě:

{\ mathbf {a}} \ klín {\ mathbf {b}} = i {\ mathbf {a}} \ krát {\ mathbf {b}}

$a \times b$ je „ anglosaský křížový produkt “, což odpovídá křížovému produktu ve francouzské vědecké literatuře, který je bohužel označovánjako vnější produkt $\land$ . Křížový produkt je tak implicitně definován jako duál externího produktu. Kanonický rozklad geometrického součinu lze tedy dát ve formě:

{\ mathbf {a}} {\ mathbf {b}} = {\ mathbf {a}} \ cdot {\ mathbf {b}} + i {\ mathbf {a}} \ times {\ mathbf {b}}

Díky této definici můžeme vytvořit vazbu mezi geometrickou algebrou a standardní vektorovou analýzou.

Prvky geometrické algebry se nazývají multivektory. Zvláštní vlastnosti pseudoscalar $i$ umožňují psát nějaký multivector $M$ o ve své rozšířené podobě: ${\ mathcal {G}} _ {3}$

M = \ alpha + {\ mathbf {a}} + i {\ mathbf {b}} + i \ beta

kde $α$ a $β$ jsou skaláry a kde $a$ a $b$ jsou vektory. Výhodou této formulace je, že redukuje množení multivektorů na vektory. Čtyři členy multivektoru jsou lineárně nezávislé, takže skalární, vektorová, bivektorová a pseudoskalární část multivektorů se během sčítání kombinují odděleně, což neplatí pro násobení. ${\ mathcal {G}} _ {3}$

Geometrická algebra je lineární prostor dimenze 1 + 3 + 3 + 1 = 2 3 = 8. ${\ mathcal {G}} _ {3}$

Rozšířená forma multivektoru má formální algebraickou strukturu „komplexního skaláru“ $α + i β$ doplněného „komplexním vektorem“ $a + i b$ , ale jakákoli fyzikální interpretace spočívá na geometrickém významu pseudoskaláře $i$ .

Korespondence S čtveřicemi

Geometrická algebra	Čtveřice	Výklad
1	1	skalární
$\ sigma _ {2} \ sigma _ {3}$	-i	yz orientovaná rovina
$\ sigma _ {3} \ sigma _ {1}$	-j	zx orientovaná rovina
$\ sigma _ {1} \ sigma _ {2}$	-k	xy orientovaná rovina

S biquaterniony

Geometrická algebra	Biquaternions	Výklad
1	1	bod definovaný jeho vektorem poloměru
$\ sigma _ {1}$	já i	orientovaná čára (vektor podél osy x)
$\ sigma _ {2}$	já j	orientovaná čára (vektor podél osy y)
$\ sigma _ {3}$	já k	orientovaná čára (vektor podél osy z)
$\ sigma _ {1} \ sigma _ {2}$	- k	rovina orientovaná na xy (bivektor)
$\ sigma _ {2} \ sigma _ {3}$	- i	yz orientovaná rovina (bivektor)
$\ sigma _ {3} \ sigma _ {1}$	- j	rovina orientovaná na zx (bivektor)
$\ sigma _ {1} \ sigma _ {2} \ sigma _ {3}$	i	objem orientovaný na xyz (trivector)

S maticovou algebrou

Geometrická algebra je analogická s algebrou konstruovanou na maticích 2 × 2 se složitými koeficienty. Tato algebra se nachází v kvantové mechanice, kterou zavedl Wolfgang Pauli , pro modelování rotace částic. Kanonické Základem této algebry se skládá z následujících osmi složitých matricích 2 x 2 Rozměry: ${\ mathcal {G}} _ {3}$

pro vektory tři Pauliho matice :

{\ displaystyle \ sigma _ {1} = \ sigma _ {x} = {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix}}, \ quad \ sigma _ {2} = \ sigma _ {y} = {\ begin {pmatrix} 0 & -i \\ i & 0 \ end {pmatrix}}, \ quad \ sigma _ {3} = \ sigma _ {z} = {\ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix}} ~;}

pro bivektory:

{\ displaystyle \ sigma _ {1} \ sigma _ {2} = \ sigma _ {xy} = {\ begin {pmatrix} i & 0 \\ 0 & -i \ end {pmatrix}}, \ quad \ sigma _ {2} \ sigma _ {3} = \ sigma _ {yz} = {\ begin {pmatrix} 0 & i \\ i & 0 \ end {pmatrix}}, \ quad \ sigma _ {3} \ sigma _ { 1} = \ sigma _ {zx} = {\ begin {pmatrix} 0 & 1 \\ - 1 & 0 \ end {pmatrix}} ~;}

pro trivektory:

{\ displaystyle \ sigma _ {1} \ sigma _ {2} \ sigma _ {3} = \ sigma _ {xyz} = {\ begin {pmatrix} i & 0 \\ 0 & i \ end {pmatrix}} ~ ;}

pro skaláry:

{\ displaystyle \ sigma _ {0} = 1 = {\ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix}}.}

Diskuse

Výrazným bodem této formulace je přirozená korespondence mezi entitami a prvky asociativní algebry. Je to proto, že geometrický součin dvou vektorů lze předefinovat, pokud jde o jejich křížový součin a jejich tečkový součin , pomocí

{\ displaystyle \ mathbf {a} \, \ mathbf {b} = \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ klín \ mathbf {b}.}

Předpokládáme, že pole skalárů v původním vektorovém prostoru je polem reálných čísel. ${\ mathcal V}$

Definice a asociativita geometrického součinu vyžaduje koncept inverze vektoru (nebo dělení vektorem). Lze tedy snadno stanovit a řešit vektorové algebraické rovnice, se kterými by bylo jinak obtížné manipulovat. Navíc získá jeden geometrický význam, který by bylo obtížné hledat, například pomocí matic. Navzdory skutečnosti, že ne všechny prvky jsou invertovatelné, lze koncept inverze rozšířit na multivektorový. Geometrická algebra nám umožňuje přímo se zabývat podprostory i jejich manipulací. Geometrická algebra je navíc formalismem bez souřadnic.

Geometrické objekty jako $a \land b$ se nazývají bivektory . Bivektor lze popsat jako rovinný segment (rovnoběžník, kruh atd.) S orientací. Bivektor představuje všechny rovinné segmenty se stejnou velikostí a směrem, bez ohledu na to, kde jsou v prostoru, který je obsahuje. Avšak jakmile je vektor $a$ nebo $b$ označen z nějakého preferovaného bodu (např. Ve fyzických problémech), je jednoznačně určena orientovaná rovina $B = a \land b$ .

Jako významný příklad, i když jednoduchý, můžeme považovat radiusový vektor $v$ jiný než nula bodu obvyklého afinního euklidovského prostoru (nezapomeňte, že radiusový vektor afinního bodu je vektor, který začíná od počátku a končí v tomto bodě). Sada všech bodů vektorových paprsků $x$ tak, že $x$ $\land$ $v$ $=$ $B$ , $B$ označující daný bivektor obsahující $v$ , určuje přímku $l$ rovnoběžnou s $v$ . Protože $B$ je orientovaná oblast , $l$ je určeno pouze zachováním zvoleného počátku. Sada všech bodů paprskových vektorů $x$ taková, že $x$ $.$ $v$ $=$ $s$ , $s$ označující daný (skutečný) skalární, určuje rovinu P kolmou k $v$ . Opět platí, že P je určeno pouze zachováním zvoleného původu. Tyto dvě informace, $B$ a $s$ , lze stanovit nezávisle na sobě. Nyní, co je radiusový vektor $y,$ který vyhovuje systému ${$ $y$ $\land$ $v$ $=$ $B$ $,$ $y$ $.$ $v$ $=$ $s$ $}$ ? Geometricky je odpověď jasná: jedná se o poloměrový vektor průsečíku $l$ a P. Geometrickou algebrou je i algebraická odpověď jednoduchá: $\ mathbb {R} ^ {3}$

{\ displaystyle \ mathbf {y} \ mathbf {v} = s + B \ Rightarrow \ mathbf {y} = (s + B) / \ mathbf {v} = (s + B) \ mathbf {v} ^ {- 1}}

kde inverze nenulového vektoru je vyjádřena $z -1 = z / z • z$ .

Poznámka: Dělení vektorem transformuje multivektor $s + B$ na součet dvou vektorů. Struktura řešení navíc nezávisí na zvoleném původu.

Jak je definováno, vnější produkt (nebo vnější produkt nebo vektorový produkt ) $\land$ generuje klasifikovaného algebry ( vnější algebry z Hermann Grassmann ) z multivectors. Multivektor je tedy přímým součtem prvků stupně k ( k- vektory ), kde k přechází z 0 ( skaláry ) do n , což je rozměr původního vektorového prostoru . Multivektory jsou zde znázorněny tučně velkými písmeny. Poznámka: Skaláry a vektory se stávají zvláštními případy multivektorů („0-vektory“ a „1-vektory“). $\ wedge ^ {n} {\ mathcal {V}} _ {n}$ ${\ mathcal V}$

Pravidlo kontrakce

Spojení mezi Cliffordovými algebrami a kvadratickými formami pochází z vlastnosti (nebo pravidla) kontrakce. Toto pravidlo také dává prostoru metriku definovanou přirozeně odvozeným interním produktem . Také v geometrické algebře v celé své obecnosti neexistuje žádné omezení hodnoty skaláru, může to být záporné, dokonce nulové (v tomto případě je možnost vnitřního součinu vyloučena, pokud se zeptáte ). $\ langle x, x \ rangle \ geq 0$

Pravidlo kontrakce může být uvedeno ve tvaru:

{\ displaystyle Q (\ mathbf {a}) = \ mathbf {a} ^ {2} = \ varepsilon _ {a} {\ zelená \ mathbf {a} \ zelená} ^ {2}}

kde $| a |$ je modul vektoru $a$ a nazývá se podpisem vektoru $a$ . To je užitečné zejména při výstavbě Minkowského prostoru (dále jen časoprostorové of relativity ) via . V tomto kontextu se nulové vektory nazývají světelné vektory, vektory negativních podpisů se nazývají vektory prostoru a vektory pozitivních podpisů se nazývají časové vektory (tyto poslední dvě jména se zaměňují při použití místo ). ${\ displaystyle \ varepsilon _ {a} = 0, \, \ pm 1}$ ${\ mathbb {R}} _ {{1,3}} \,$ ${\ mathbb {R}} _ {{3,1}}$ ${\ mathbb {R}} _ {{1,3}} \,$

Výrobky pro vnitřní i venkovní použití

Obvykle dot produkt a součin tradiční vektorové algebry (sur ) najít své místo v geometrické algebře jako vnitřní produkt ${\ mathbb {R}} ^ {3} \,$ ${\ mathcal {G}} _ {3} \,$

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ frac {1} {2}} (\ mathbf {a} \ mathbf {b} + \ mathbf {b} \ mathbf {a})}

(který je symetrický) a externí produkt

{\ mathbf {a}} \ wedge {\ mathbf {b}} = {\ frac {1} {2}} ({\ mathbf {a}} {\ mathbf {b}} - {\ mathbf {b}} {\ mathbf {a}})

{\ mathbf {a}} \ times {\ mathbf {b}} = - i ({\ mathbf {a}} \ klín {\ mathbf {b}})

(což je antisymetrické). Rozdíl mezi axiálními a polárními vektory, který je ve vektorové algebře nejasný, je přirozený v geometrické algebře, kde je vyjádřen jako rozdíl mezi vektory a bivektory (stupeň dva prvky). $I$ zde je pseudoscalar jednotka euklidovské 3-prostoru, který zavádí dualitu mezi vektory a bivectors, a je tak pojmenovaný protože předpokládané majetku $i 2 = -1$ .

Zatímco křížový produkt lze definovat pouze v trojrozměrném prostoru, vnitřní a vnější produkty lze zobecnit na jakoukoli dimenzi.

Dovolit být vektorem a homogenním multivektorem stupně k . Jejich interní produkt je pak: a jejich externí produkt je ${\ mathbf {a}}, \, {\ mathbf {A}} _ {{\ langle k \ rangle}}$ ${\ mathbf a} \ cdot {\ mathbf A} _ {{\ langle k \ rangle}} = {1 \ nad 2} \, \ left ({\ mathbf a} \, {\ mathbf A} _ {{\ langle k \ rangle}} + (- 1) ^ {{k + 1}} \, {\ mathbf {A}} _ {{\ langle k \ rangle}} \, {\ mathbf {a}} \ right) = (- 1) ^ {{k + 1}} {\ mathbf A} _ {{\ langle k \ rangle}} \ cdot {\ mathbf {a}}$

{\ displaystyle \ mathbf {a} \ klín \ mathbf {A} _ {\ langle k \ rangle} = {1 \ nad 2} \, \ left (\ mathbf {a} \, \ mathbf {A} _ {\ langle k \ rangle} - (- 1) ^ {k + 1} \, \ mathbf {A} _ {\ langle k \ rangle} \, \ mathbf {a} \ right) = (- 1) ^ {k} \ mathbf {A} _ {\ langle k \ rangle} \ klín \ mathbf {a}.}

Konformní geometrická algebra

Vektorový prostor, i když je opatřen skalárním součinem, není sám o sobě vhodný pro modelování obvyklého prostoru, to znamená euklidovského prostoru. Je skutečně nutné rozlišovat pojmy bodů a vektorů . K tomu existuje několik modelů, nejpozoruhodnější je afinní prostor a projektivní geometrie .

Zatímco projektivní geometrie přidává další dimenzi, čímž se z obvyklého prostoru stává hyperplán , konformní geometrická algebra je model euklidovského prostoru založený na geometrické algebře, která nepřidává jednu, ale dvě další dimenze. Tyto dvě dimenze, které mají strukturu Minkowského prostoru, se z obvyklého prostoru stávají horosférou .

Aplikace

Omezená relativita a elektromagnetismus

Užitečným příkladem je a způsob jeho generování příklad geometrické algebry, kterou Hestenes nazývá časoprostorová algebra . Tato algebra je vybavena základnou vektorů, které jsou nejčastěji označovány jako: ${\ mathbb {R}} _ {{3,1}}$ ${\ mathcal {G}} _ {{3,1}}$ $({\ mathbf {\ gamma}} _ {0}, {\ mathbf {\ gamma}} _ {1}, {\ mathbf {\ gamma}} _ {2}, {\ mathbf {\ gamma}} _ { 3})$

{\ mathbf {\ gamma}} _ {0} ^ {2} = - 1, \ qquad {\ mathbf {\ gamma}} _ {1} ^ {2} = {\ mathbf {\ gamma}} _ {2 } ^ {2} = {\ mathbf {\ gamma}} _ {3} ^ {2} = + 1

$({\ mathbf {\ gamma}} _ {1}, {\ mathbf {\ gamma}} _ {2}, {\ mathbf {\ gamma}} _ {3})$ představuje ortonormální základ obvyklého euklidovského prostoru. je vektor oddělující dvě události časové jednotky. ${\ mathbf {\ gamma}} _ {0}$

Elektromagnetické pole , v této souvislosti, se ukáže být bivectorial pole , pro které elektrická a magnetická pole charakterizují časoprostorových (to znamená, obsahující časovou směr) a čistě prostorové části (bivectors směrována dvěma směry obvyklý prostor):

F = ({\ mathbf {E}} + i {\ mathbf {B}}) {\ mathbf {\ gamma}} _ {0}

nebo podrobněji:

{\ displaystyle {\ begin {aligned} F & = (\ mathbf {E} + \ mathbf {\ gamma} _ {0} \ mathbf {\ gamma} _ {1} \ mathbf {\ gamma} _ {2} \ mathbf {\ gamma} _ {3} \ mathbf {B}) \ mathbf {\ gamma} _ {0} \\ & = \ mathbf {E} \ mathbf {\ gamma} _ {0} - \ mathbf {B} \ mathbf {\ gamma} _ {1} \ mathbf {\ gamma} _ {2} \ mathbf {\ gamma} _ {3} \\ & = E ^ {k} \ mathbf {\ gamma} _ {k} \ mathbf {\ gamma} _ {0} -B ^ {k} \ mathbf {\ gamma} _ {k} \ mathbf {\ gamma} _ {1} \ mathbf {\ gamma} _ {2} \ mathbf {\ gamma } _ {3} \\ & = E ^ {k} \ mathbf {\ gamma} _ {k} \ mathbf {\ gamma} _ {0} - (B ^ {1} \ mathbf {\ gamma} _ {2 } \ mathbf {\ gamma} _ {3} + B ^ {2} \ mathbf {\ gamma} _ {3} \ mathbf {\ gamma} _ {1} + B ^ {3} \ mathbf {\ gamma} _ {1} \ mathbf {\ gamma} _ {2}). \ End {zarovnáno}}}

Pak můžeme ukázat, že Maxwellovy rovnice překládají skutečnost, že aktuální kvadrivektor pochází z tohoto bivektorového pole: $J = \ rho {\ mathbf {\ gamma}} _ {0} + {\ mathbf {j}}$

\ nabla F = J

$\ nabla$ se zde vztahuje ke gradientu ve smyslu geometrické algebře, to znamená, že, jak je definováno výše: . Podrobné vyjádření tohoto operátora vyžaduje výpočet . Jako z definice máme , takže je napsáno: $\ nabla = {\ mathbf {\ gamma}} ^ {\ mu} \ částečný _ {\ mu}$ ${\ mathbf {\ gamma}} ^ {0}$ ${\ mathbf {\ gamma}} ^ {0} \ cdot {\ mathbf {\ gamma}} _ {0} = 1$ ${\ mathbf {\ gamma}} ^ {0} = - {\ mathbf {\ gamma}} _ {0}$ $\ nabla$

{\ displaystyle \ nabla = - \ mathbf {\ gamma} _ {0} \ částečné _ {0} + \ mathbf {\ gamma} _ {1} \ částečné _ {1} + \ mathbf {\ gamma} _ {2 } \ částečné _ {2} + \ mathbf {\ gamma} _ {3} \ částečné _ {3}.}

Lorentzova síla je napsáno , kde a jsou elektromagnetické náboje a rychlost čtyřnásobný , tak, že pohybová rovnice je napsáno, s ohledem na Quadri impuls : ${\ displaystyle q \ mathbf {u} \ cdot F}$ $q$ ${\ mathbf u}$ $\ mathbf {p}$

{\ displaystyle {\ frac {d} {d \ tau}} \ mathbf {p} = q \ mathbf {u} \ cdot F.}

K zrychlení v tomto metrickém Lorentzian prostoru mají stejný výraz jako rotace v euklidovském prostoru, kde je samozřejmě bivector generované času a směrů prostoru zapojených, s ohledem na v euklidovském případě, že se jedná o bivector generované ve dvou směrech vesmíru, posílení „analogie“ kvazi-identity. $e ^ {{{\ mathbf {\ beta}}}}$ ${\ mathbf {\ beta}}$

Infografika

V roce 2014 existovala alespoň jedna společnost využívající geometrickou algebru v počítačové grafice , konkrétněji v odvětví videoher . Jedná se o Geomerics (en) , založenou v roce 2005 zejména Chrisem JL Doranem (en) , doktorem fyziky. Doran řekl, že založil Geomerics právě s cílem najít další způsoby, jak upozornit vědeckou komunitu na metody geometrické algebry.

v Březen 2014Společnost Unity Technologies (in) zahájila spolupráci s Geomerics za účelem integrace jejich vykreslovacího modulu globálního osvětlení v reálném čase do páté verze enginu Unity .

Bibliografie

(en) David Hestenes (2003), „Přednáška Oersted Medal 2002: Reforming the Mathematical Language of Physics“ (PDF), Am. J. Phys. , 71 (2)
(en) David Hestenes (2003), „Spacetime Physics with Geometric Algebra“ (PDF), Am. J. Phys. , 71 (6)
(en) David Hestenes (1999), „New Foundations for Classical Mechanics “ , Springer Verlag, ( ISBN 978-0-7923-5302-7 )
(en) Chris Doran, Anthony Lasenby (2003), „Geometric Algebra for Physicist“, Cambridge University Press, ( ISBN 978-0-521-71595-9 )
(en) Leo Dorst, Daniel Fontijne, Stephen Mann (2007), „Geometric Algebra for Computer Science“, Elsevier / Morgan Kaufman, ( ISBN 978-0-12-369465-2 )
Gaston Casanova (1976), "L 'algebra vector", Presses Universitaires de France, ( ISBN 978-2130343059 )
Georges Pagis (2018), „GA Maths Physique pour demain“, ( ISBN 978-1980691389 )

Reference

(fr) Tento článek je částečně nebo zcela převzat z článku anglické Wikipedie s názvem „ Geometrická algebra “ ( viz seznam autorů ) .
(en) WE Baylis (ed.), Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering , Boston, Birkhäuser, 1996
(en) Chris Doran, Geometrická algebra a její aplikace na matematickou fyziku , PhD , Sidney Sussex College , 1994
(en) David Hestenes a Garret Sobczyk, Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics , Springer ,1984( DOI 10.1007 / 978-94-009-6292-7 )
(en) David Hestenes, „Jednotný jazyk pro matematiku a fyziku“ , JSR Chisholm a AK Common, Clifford Algebras a jejich aplikace v matematické fyzice , Reidel,1986( DOI 10.1007 / 978-94-009-4728-3_1 , číst online ) , s. 1-23
(en) David Hestenes, Hongbo Li a Alyn Rockwood, „Nové algebraické nástroje pro klasickou geometrii“ , Gerald Sommer, Geometric Computing s Clifford Algebras , Springer,2001( DOI 10.1007 / 978-3-662-04621-0_1 , číst online ) , s. 3-26
(en) Alan McDonald , „ An Survey of Geometric Algebra and Geometric Calculus “ , na Luther College (Iowa) (en) ,2015
(en) Geometrická algebra pro elektrotechnické a elektronické inženýry , digitální knihovna IEEE
(en) Elektromagnetismus pomocí geometrické algebry versus komponenty

Poznámky

Jinými slovy: každý prvek geometrické algebry je součtem produktů prvků vektorového podprostoru.
Hestenes 1986 , str. 5: Směrovaná čísla jsou definována implicitně určením pravidel pro přidávání a násobení vektorů. Konkrétně předpokládáme, že vektory generují asociativní algebru, ve které je čtverec každého vektoru skalární. ( "Směrovaná čísla jsou definována implicitně určením pravidel pro sčítání a množení vektorů. Konkrétně předpokládáme, že vektory generují asociativní algebru, ve které je čtverec vektoru skalární." )
Hestenes 1986 , str. 7: Mám polovinu mysli, abych úplně postavil komplex Cliffordských algeber mimo zákon, protože imaginární skaláry nemají přirozenou geometrickou interpretaci a jejich algebraické rysy již existují ve skutečných cliffordských algebrách. O složitých Cliffordských algebrách však již existuje značná literatura a mají některé formální výhody. ( „Jsem v pokušení úplně zakázat používání složitých Cliffordových algeber, protože imaginární skaláry nemají žádnou přirozenou geometrickou interpretaci a jejich algebraické vlastnosti již existují ve skutečných Cliffordových algebrách. O složitých Cliffordových algebrách však již existuje značná literatura a oni mít nějaké formální výhody. “ )
Předpokládáme, zde a v celém zbytku výrobku, že charakteristika z je odlišný od 2, to znamená, že 2 je jiné než nula, a proto invertibilní. $\ mathbb {K}$
Slovo lame zde bylo vybráno k překladu anglického výrazu blade používaného Hestenesem, ale je třeba poznamenat, že neexistuje žádný francouzský odkaz, který by tuto volbu překladu mohl podpořit.
Termín stupeň se v tomto článku používá k překladu anglického slova stupeň používaný Hestenesem, které se také nachází ve výrazu absolvovaná algebra . Alternativou je francouzský termín stupeň . Ve své první knize Space Time Algebra použil Hestenes termín stupeň , ale ve svých pozdějších pracích a článcích použil termín známka .
Někdy se také nazývá k -multivector.
(in) Ian Bell , multivektorové metody .
Tento zápis by neměla být zaměňována s „ K -uple kartézský součin z na sebe“. Abychom to nezjistili, dalo by se to napsat . $\ mathcal {G}$ $({\ mathcal {G}}) ^ {k}$
Hestenes, Li a Rockwood 2001 .
Zápis , tj. Použití velkého písmene jako dolního indexu, je zde vypůjčen z McDonald's 2015 . Zvolili jsme však nepoužívat tučné písmo pro symbol, pokud je používán, protože neoznačuje vektor, ale geometrický součin vektorů. $e_ {J}$ $E$
Existence unitárních pseudoskalářů není zaručena. Jinak se říká, že je zdegenerovaný . V tomto článku, a pokud není uvedeno jinak, se nacházíme v nedegenerovaném případě. ${\ mathcal {V}} ^ {n}$
Ectomorphism zde byla zvolena přeložit Hestenes' termín outermorphism . Francouzsky mluvící vědecké použití ve skutečnosti upřednostňuje řecké a latinské kořeny pro složení nových slov. Řecká předpona ecto-, což znamená „venku“, se proto jeví jako vhodné překládat vnější- .
Rozhodli jsme se nepoužívat zde symbol k vyjádření kolinearity. Ve skutečnosti se používá k vyjádření paralelismu , což je pojem používaný hlavně v afinní geometrii, který podle Euklida označuje dvě koplanární linie, které se nesetkávají, když jsou prodlouženy na obou stranách do nekonečna. Upřednostňovali jsme symbol vyjadřující proporcionalitu . $\ paralelní$ $\ paralelní$ $\ propto$
Hestenes 1986 , str. 7 neváhá prozradit, že klasické definice tenzorových a externích algeber a (multiplikátů) Cliffordových algeber jsou pro něj hermetické: „ Cliffordské algebry jsou někdy definovány jako určité ideály v tenzorových algebrách [sic]. Na tom není logicky nic špatného, ale tvrdím, že je lepší matematický design obrátit proces a zavést tenzor jako multilineární funkce definované na Cliffordových algebrách [re-sic]. „ ( “ Clifford algebry jsou někdy definovány určité ideály z tenzorových algebry . Na tom není nic s tím logicky špatně, ale domnívám se, že lepší matematická konstrukce je snaha o zvrácení procesu a zavést tenzory jako funkce. Multinear definovaný přes Clifford algebry. " $\ mathcal {V}$ $\ mathcal {V}$
(in) Počítačová grafika využívající konformní geometrickou algebru , Richard J. Wareham, PhD, s. 26.
Geometrická algebra pro fyziky , Chris Doran, část 2.4.2 „Bivektorová algebra“
Pojem „obraceč“ je zde vybrán k překladu anglického výrazu rotor . Alternativou je „rotátor“.
Exponenciálu je zde třeba chápat v algebraickém smyslu, to znamená . ${\ displaystyle e ^ {i \ theta} = \ sum _ {n \ geq 0} {\ frac {(i \ theta) ^ {n}} {n!}}}$
Časoprostorová algebra . Podívejte se na časoprostorový článek (algebraická struktura) .
Konvence ${\ mathbf {\ gamma}} _ {0} ^ {2} = + 1, \ qquad {\ mathbf {\ gamma}} _ {1} ^ {2} = {\ mathbf {\ gamma}} _ {2 } ^ {2} = {\ mathbf {\ gamma}} _ {3} ^ {2} = - 1$ se také velmi často používá.
(in) „ Unity 5 Announced at GDC 2014 Pre-Order Begins “ .